Contacto entre sólidos
De Laplace
| Línea 1: | Línea 1: | ||
| + | <!-- | ||
__TOC__ | __TOC__ | ||
==Pares cinemáticos== | ==Pares cinemáticos== | ||
| Línea 123: | Línea 124: | ||
<center>[[Archivo:cardan-horizontal.png|300px]]{{qquad}}{{qquad}}[[Archivo:cardan-oblicuo.png|300px]]</center> | <center>[[Archivo:cardan-horizontal.png|300px]]{{qquad}}{{qquad}}[[Archivo:cardan-oblicuo.png|300px]]</center> | ||
| - | + | --> | |
==Deslizamiento, rodadura y pivotamiento== | ==Deslizamiento, rodadura y pivotamiento== | ||
Revisión de 22:56 10 dic 2019
Contenido |
1 Par prismático (corredera rectangular)
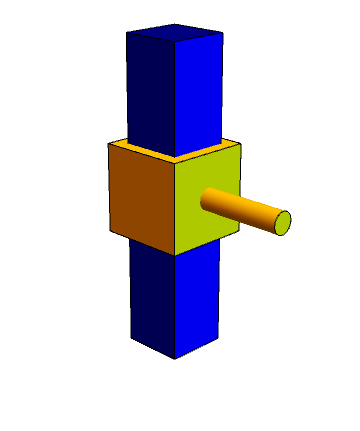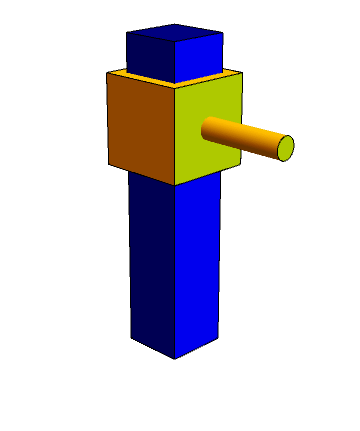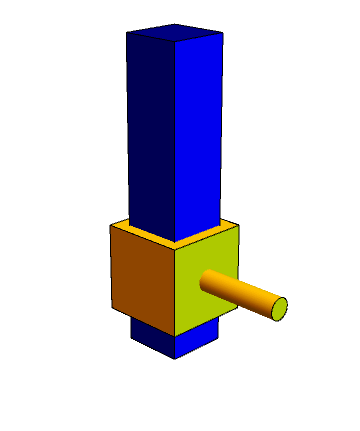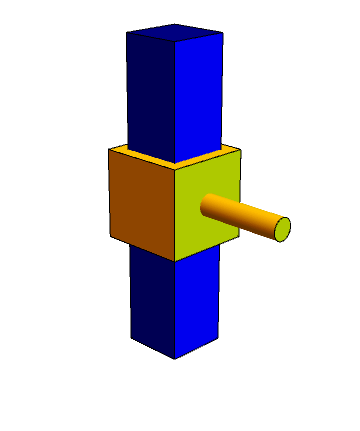
El sólido 2 puede deslizarse a lo largo de un cierto eje, pero no puede girar en torno a él (un único grado de libertad relativa)
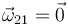
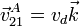
- El movimiento relativo en este caso es una traslación, siendo la velocidad de todos los puntos en la dirección fijada por el vínculo.
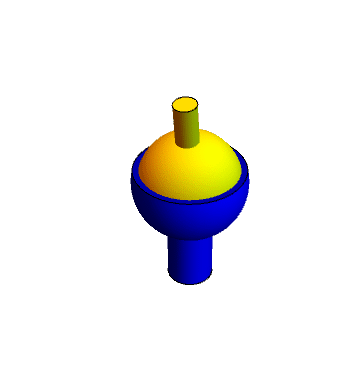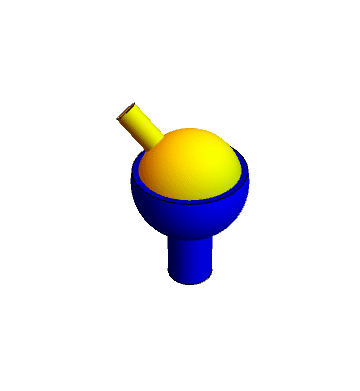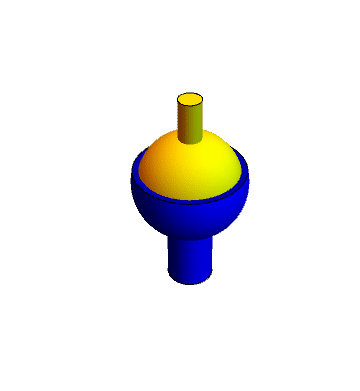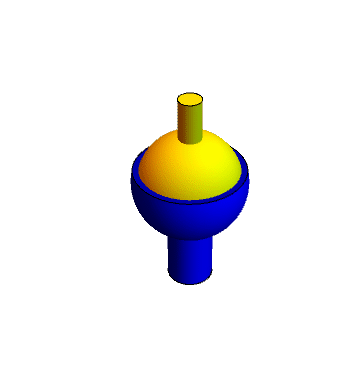
2 Par esférico (rótula o articulación)
El punto A (centro de la rótula) es un punto fijo en el movimiento relativo de los dos sólidos. El sólido 2 puede girar libremente (pero no trasladarse) respecto al 1. Por ello
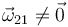
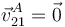
El movimiento relativo del sólido 2 respecto al 1 es siempre una rotación pura en torno a un eje que pasa por A. Existen tres grados de libertad relativa rotacionales.
3 Par plano
El punto A solo puede deslizar sobre la superficie del sólido 1, y el sólido puede girar en torno al eje perpendicular a la superficie de contacto.
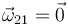
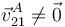
El movimiento relativo del sólido 2 respecto al 1 es un movimiento plano, con tres grados de libertad.
4 Par rígido (empotramiento, voladizo o cantilever)
Los dos sólidos forman en realidad uno solo, ya que en el punto de contacto la unión es rígida
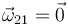
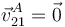
El sólido 2 se encuentra en reposo respecto al 1 (cero grados de libertad relativa).
5 Resumen
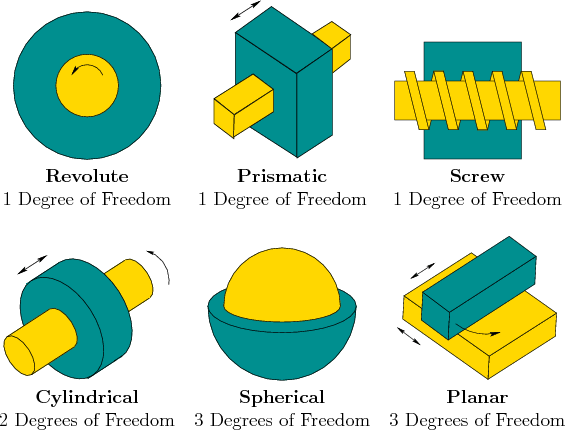
6 Combinaciones de pares. Junta cardán
Estos pares pueden combinarse entre sí, aumentando (o reduciendo en su caso) el número de grados de libertad relativos. Así, por ejemplo, una junta cardán o junta universal combina dos pares de revolución, permitiendo orientaciones arbitrarias del sólido 2 respecto al 1. Por ello, es común en todo tipo de brazos articulados. En este sentido se asemeja a una rótula, con la diferencia de que no permite la rotación en torno a uno de los tres ejes posibles.
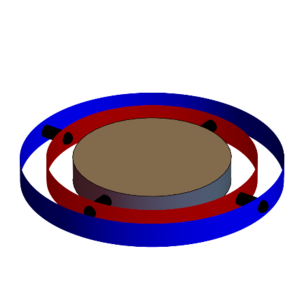
El mismo principio se aplica a la suspensión cardán (gimbal en inglés, término que también se usa en castellano) en la que mediante dos ejes perpendiculares montados en anillos concéntricos (o sistemas equivalentes) es posible orientar un dispositivo, como un telescopio o un brazo robótico.
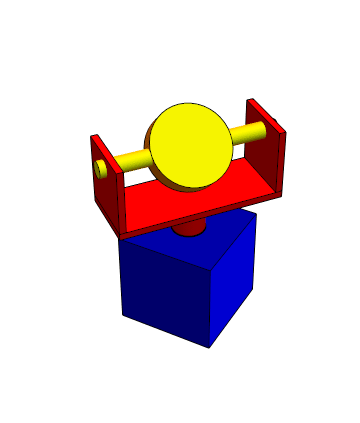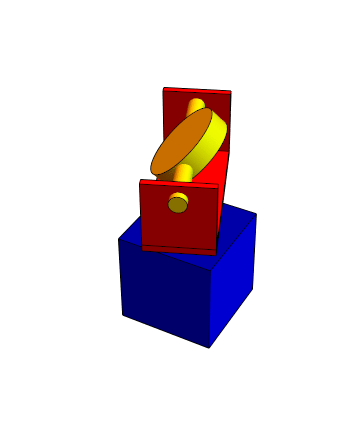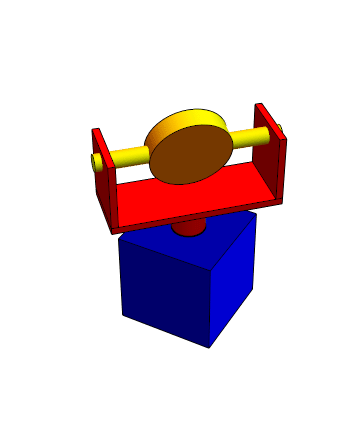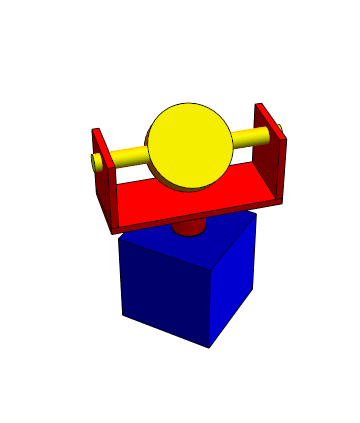
También se emplea, a la inversa, para estabilizar un sistema, como una brújula, que debe permanecer horizontal mientras su entorno (un barco) está cambiando su orientación.
-->
7 Deslizamiento, rodadura y pivotamiento
Cuando tenemos dos sólidos en contacto, tales que un punto del sólido 2 se encuentra sobre una superficie del sólido 1 (por ejemplo, una pelota sobre una mesa), es posible que el punto de contacto esté en reposo relativo (como en el par esférico instantáneo o el de revolución instantáneo), o que no lo esté. Cuando el punto de contacto posee una cierta velocidad se dice que existe deslizamiento entre los sólidos. Se define la velocidad de deslizamiento entre los sólidos como la del punto de contacto,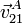 
Esta velocidad será necesariamente tangente a la superficie y por tanto ortogonal a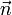 
, el vector normal a la superficie.
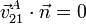
Por otra parte, la velocidad angular puede tener una parte en la dirección perpendicular a la superficie, esto es, el sólido 2 posee un giro en torno a un eje perpendicular a la superficie Y paralelo, por tanto, al vector 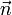). Cuando esto ocurre se dice que el sólido 2 pivota sobre el uno y esta componente de la velocidad angular se denomina velocidad angular de pivotamiento.
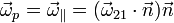
Además de la posible parte perpendicular a la superficie, la velocidad angular posee una parte tangente a la superficie (y perpendicular a 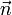, por tanto), de forma que el sólido 2 posee una componente de giro a en torno a un eje paralelo a la superficie. Se dice entonces que tenemos rodadura en el punto de contacto, siendo la velocidad angular de rodadura
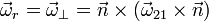
En un movimiento general tendremos las tres componentes: rodadura, deslizamiento y pivotamiento, siendo la velocidad de cualquier punto del sólido 2
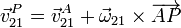
No obstante, en muchas ocasiones algunas de estas componentes son nulas. Así, tenemos los casos:
- Rodar y pivotar sin deslizar
- La velocidad de deslizamiento es nula
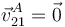
- El movimiento instantáneo del sólido 2 es una rotación pura en torno a un cierto eje que pasa por el punto de contacto. Este es el movimiento que describe habitualmente, por ejemplo, una bola que se mueve sobre una superficie horizontal con rozamiento.
- Rodar sin deslizar
- Si no se indica que existe pivotamiento, se supone que este es nulo, en este caso, la velocidad angular
es tangente a la superficie del sólido 1. El movimiento relativo es una rotación pura alrededor de un eje tangente a la superficie de 1. Este es el movimiento de un disco que rueda sobre un plano. Así, respecto al suelo, una rueda de un coche no rueda en torno a su eje, sino en torno a un eje que pasa por el punto donde toca el suelo y es tangente a este.
- Deslizamiento sin rodadura
- La velocidad angular es nula (se supone que tampoco hay pivotamiento) y el sólido 2 se traslada respecto al 1 con la velocidad
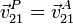
- Esto ocurre, por ejemplo, cuando se arrastra un cierto sólido (una caja, por ejemplo) sobre otro.
Estas situaciones pueden venir obligadas por los pares cinemáticos. Así un par de deslizamiento implica deslizamiento sin rodadura ni pivotamiento; un par esférico, rodadura y pivotamiento sin deslizamiento; un par de revolución, rodadura sin deslizamiento ni pivotamiento; etc.
| Deslizamiento | Rodadura | Pivotamiento |
|---|---|---|
| 
| 
|
