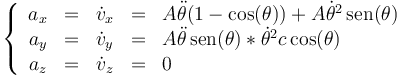Movimiento cicloidal (CMR)
De Laplace
(Diferencias entre revisiones)
| Línea 20: | Línea 20: | ||
v_z & = & \dot{z} & = & 0\end{array}\right.</math></center> | v_z & = & \dot{z} & = & 0\end{array}\right.</math></center> | ||
| + | Derivando de nuevo obtenemos la aceleración. Por componentes: | ||
| + | |||
| + | <center><math>\left\{\begin{array}{rcccl} | ||
| + | a_x & = & \dot{v}_x & = & A\ddot{\theta}(1-\cos(\theta))+A\dot{\theta}^2\,\mathrm{sen}(\theta) \\ | ||
| + | a_y & = & \dot{v}_y & = & A\ddot{\theta}\,\mathrm{sen}(\theta)*\dot{\theta}^2c\cos(\theta)\\ | ||
| + | a_z & = & \dot{v}_z & = & 0\end{array}\right.</math></center> | ||
==Aceleración tangencial y normal== | ==Aceleración tangencial y normal== | ||
| - | ==Centros de curvatura== | + | ==Centros de curvatura== |
==Distancia recorrida== | ==Distancia recorrida== | ||
[[Categoría:Problemas de cinemática de la partícula (CMR)]] | [[Categoría:Problemas de cinemática de la partícula (CMR)]] | ||
Revisión de 16:05 9 nov 2020
Contenido |
1 Enunciado
Un punto exterior de una rueda que rueda sin deslizar describe una cicloide
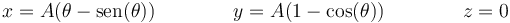
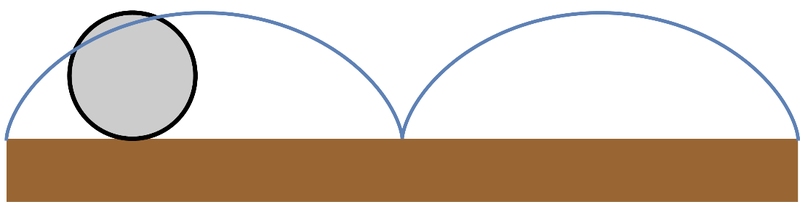
- Determine la velocidad y aceleración de la partícula en función de θ y sus derivadas respecto al tiempo. ¿Cuánto valen
y 
en el momento en que el punto se halla en lo más alto de la rueda?
- Halle la aceleración tangencial y normal.
- Calcule la posición de los centros de curvatura.
- Halle la distancia recorrida por el punto cuando la rueda da una vuelta completa.
2 Velocidad y aceleración
Las componentes cartesianas de la velocidad las hallamos aplicando la regla de la cadena
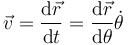
Separando por componentes
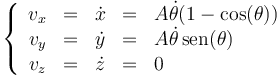
Derivando de nuevo obtenemos la aceleración. Por componentes:
