Movimiento cicloidal (CMR)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Un punto exterior de una rueda que rueda sin deslizar describe una cicloide <center><math>x=R(\theta-\mathrm{sen}(\theta))\qquad\qquad y=R(1-\cos(\theta))\qq…') |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
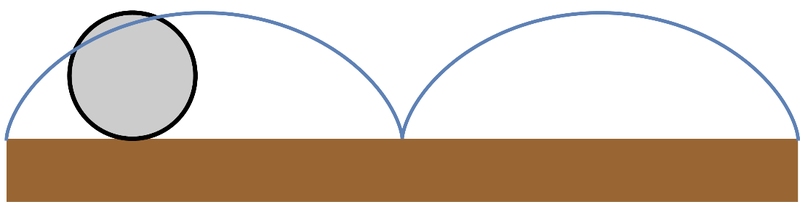
Un punto exterior de una rueda que rueda sin deslizar describe una cicloide | Un punto exterior de una rueda que rueda sin deslizar describe una cicloide | ||
| - | <center><math>x= | + | <center><math>x=A(\theta-\mathrm{sen}(\theta))\qquad\qquad y=A(1-\cos(\theta))\qquad\qquad z=0</math></center> |
| - | <center>[[Archivo:movimiento-cicloidal.png| | + | <center>[[Archivo:movimiento-cicloidal.png|800px]]</center> |
# Determine la velocidad y aceleración de la partícula en función de θ y sus derivadas respecto al tiempo. ¿Cuánto valen <math>\vec{v}</math> y <math>\vec{a}</math> en el momento en que el punto se halla en lo más alto de la rueda? | # Determine la velocidad y aceleración de la partícula en función de θ y sus derivadas respecto al tiempo. ¿Cuánto valen <math>\vec{v}</math> y <math>\vec{a}</math> en el momento en que el punto se halla en lo más alto de la rueda? | ||
# Halle la aceleración tangencial y normal. | # Halle la aceleración tangencial y normal. | ||
# Calcule la posición de los centros de curvatura. | # Calcule la posición de los centros de curvatura. | ||
# Halle la distancia recorrida por el punto cuando la rueda da una vuelta completa. | # Halle la distancia recorrida por el punto cuando la rueda da una vuelta completa. | ||
| + | |||
==Velocidad y aceleración== | ==Velocidad y aceleración== | ||
==Aceleración tangencial y normal== | ==Aceleración tangencial y normal== | ||
Revisión de 09:25 23 oct 2017
Contenido |
1 Enunciado
Un punto exterior de una rueda que rueda sin deslizar describe una cicloide
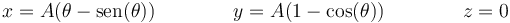
- Determine la velocidad y aceleración de la partícula en función de θ y sus derivadas respecto al tiempo. ¿Cuánto valen
y 
en el momento en que el punto se halla en lo más alto de la rueda?
- Halle la aceleración tangencial y normal.
- Calcule la posición de los centros de curvatura.
- Halle la distancia recorrida por el punto cuando la rueda da una vuelta completa.
