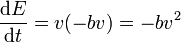Oscilador amortiguado
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Enunciado== Un oscilador amortiguado experimenta una fuerza de rozamiento viscoso <math>\mathbf{F}_r=-b \mathbf{v}</math>, de forma que su ecuación de movimiento, para un movimient...) |
(→Disipación de la energía) |
||
| Línea 22: | Línea 22: | ||
==Solución== | ==Solución== | ||
===Disipación de la energía=== | ===Disipación de la energía=== | ||
| + | Para ver que en presencia de rozamiento la energía mecánica se va perdiendo progresivamente, simplemente calculamos la derivada de la energía respecto al tiempo, para ver su signo. | ||
| + | |||
| + | Aplicando el mismo método que en el [[Solución general del MAS|caso sin rozamiento]] | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}E}{\mathrm{d}t}=mv\,\frac{\mathrm{d}v}{\mathrm{d}t}+kx\,\frac{\mathrm{d}x}{\mathrm{d}t} = v\left(ma+kx\right)</math></center> | ||
| + | |||
| + | De acuerdo con al ecuación de movimiento para el oscilador armónico con rozamiento | ||
| + | |||
| + | <center><math>ma + kx = -bv\,</math></center> | ||
| + | |||
| + | así que nos queda | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}E}{\mathrm{d}t}=v(-bv) = -bv^2</math></center> | ||
| + | |||
===Soluciones exponenciales=== | ===Soluciones exponenciales=== | ||
===Oscilaciones amortiguadas=== | ===Oscilaciones amortiguadas=== | ||
===Casos particulares=== | ===Casos particulares=== | ||
[[Categoría:Problemas de movimiento oscilatorio]] | [[Categoría:Problemas de movimiento oscilatorio]] | ||
Revisión de 20:37 8 feb 2009
Contenido |
1 Enunciado
Un oscilador amortiguado experimenta una fuerza de rozamiento viscoso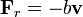 
, de forma que su ecuación de movimiento, para un movimiento unidimensional es
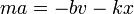
- Demuestre que la energía mecánica
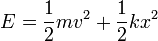
- Si buscamos una solución particular de la forma x = Ae − λt, calcule los dos valores que puede tener λ. La solución general será una combinación de las dos posibilidades:
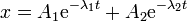
- ¿Cuál es el máximo valor de b para que haya oscilaciones? ¿cómo es el movimiento si b supera ese valor?
- Considere el caso particular de una partícula de masa
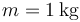se encuentra sujeta a un muelle de constante
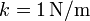, existiendo un rozamiento b. Determine la posición en cualquier instante si se impulsa desde la posición de equilibrio con velocidad 
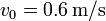si (a) 
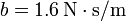$; (b) 
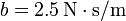, (c)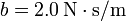 
.
2 Solución
2.1 Disipación de la energía
Para ver que en presencia de rozamiento la energía mecánica se va perdiendo progresivamente, simplemente calculamos la derivada de la energía respecto al tiempo, para ver su signo.
Aplicando el mismo método que en el caso sin rozamiento
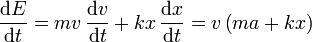
De acuerdo con al ecuación de movimiento para el oscilador armónico con rozamiento
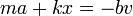
así que nos queda
