Oscilaciones de un acelerómetro
De Laplace
(→Deslizamiento por un plano) |
(→Movimiento horizontal) |
||
| Línea 44: | Línea 44: | ||
<math>\mathbf{g}=-g\mathbf{j}</math>{{qquad}}{{qquad}}<math>\mathbf{a}_0=a_0\mathbf{i}</math>{{qquad}}{{qquad}}<math>\mathbf{g}_\mathrm{ef}=-a_0\mathbf{i}-g\mathbf{j}</math></center> | <math>\mathbf{g}=-g\mathbf{j}</math>{{qquad}}{{qquad}}<math>\mathbf{a}_0=a_0\mathbf{i}</math>{{qquad}}{{qquad}}<math>\mathbf{g}_\mathrm{ef}=-a_0\mathbf{i}-g\mathbf{j}</math></center> | ||
| - | Al ser oblicua la dirección de la gravedad efectiva, lo mismo ocurrirá con la posición de equilibrio del péndulo. La inclinación de este, en reposo en el sistema acelerado permite medir directamente la aceleración, ya que se cumplirá | + | [[Imagen:camiona0.png|left]]Al ser oblicua la dirección de la gravedad efectiva, lo mismo ocurrirá con la posición de equilibrio del péndulo. La inclinación de este, en reposo en el sistema acelerado permite medir directamente la aceleración, ya que se cumplirá |
<center><math>\mathrm{tg}\,\theta_\mathrm{eq}=\frac{a_0}{g}</math></center> | <center><math>\mathrm{tg}\,\theta_\mathrm{eq}=\frac{a_0}{g}</math></center> | ||
Revisión de 20:41 8 feb 2009
Contenido |
1 Enunciado
Un acelerómetro consiste en un péndulo que se cuelga del techo de un vehículo, el cual se mueve con una cierta aceleración.
- Suponga que este vehículo es la cabina de un ascensor que se mueve verticalmente con aceleración constante a0. El periodo de oscilación del péndulo, ¿aumenta o disminuye? ¿En qué proporción respecto a su valor en reposo?
- Si el vehículo es un camión que avanza horizontalmente con aceleración a0, ¿qué ángulo con la vertical formará el péndulo en equilibrio? ¿En qué proporción varía el periodo de oscilación para este péndulo?
- Si el vehículo es una caja que desliza libremente por un plano inclinado 30°, ¿qué ángulo con el suelo de la caja formará el hilo del péndulo en equilibrio? ¿En qué proporción varía el periodo de oscilación?
2 Solución
La forma más sencilla de resolver estos casos es introduciendo las fuerzas de inercia. Cuando una partícula se encuentra en un sistema que se mueve con aceleración lineal 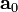 , la dinámica de la partícula se puede simplificar tratando el sistema de referencia acelerado como inercial y añadiendo una fuerza ficticia de inercia, de valor
, la dinámica de la partícula se puede simplificar tratando el sistema de referencia acelerado como inercial y añadiendo una fuerza ficticia de inercia, de valor

Cuando la aceleración del sistema es constante, esta fuerza de inercia equivale a decir que la partícula se encuentra sometida a una gravedad efectiva
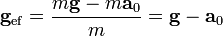
donde tanto la gravedad como la aceleración deben ser tratados vectorialmente.
2.1 Movimiento vertical
En el caso del ascensor la gravedad y la aceleración del sistema son colineales. Tomando el eje Y el marcado por la vertical hacia arriba
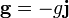
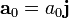
y la gravedad efectiva es
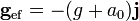
Esto quiere decir que la gravedad efectiva es mayor (en módulo) que la real si el ascensor acelera hacia arriba (por ejemplo, al emepezar a subir), y menor cuando acelera hacia abajo (por ejemplo, al llegar a la planta superior). Nótese que el sentido de la aceleración no tiene por qué coincidir con el de la velocidad: el ascensor puede estar subiendo (velocidad hacia arriba), pero frenando (aceleración hacia abajo).
El periodo de las oscilaciones del péndulo lo dará la gravedad efectiva
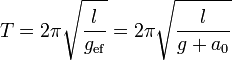
Comparando este periodo con su valor en ausencia de aceleración
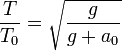
El periodo acelerado será menor que el no acelerado si el ascensor acelera hacia arriba (aumenta el peso efectivo) y mayor en caso contrario.
2.2 Movimiento horizontal
Si el acelrómetro está montado en un vehículo que se mueve horizontalmente, ya el peso y la fuerza de inercia actúan en direcciones perpendiculares, por lo que se requiere la suma vectorial
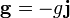
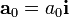
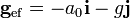
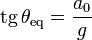
(hacia atrás si el camión acelera hacia adelante y viceversa)
Si el péndulo oscila en torno a esta posición, el periodo de sus oscilaciones será
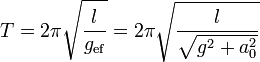
y la proporción con el periodo no acelerado
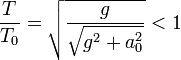
En este caso, tanto si acelera hacia adelante como hacia atrás, el periodo de oscilación es menor que en el caso no acelerado.
2.3 Deslizamiento por un plano
Si el péndulo está montado en el techo de un cajón que resbala libremente por un plano, la aceleración del movimiento será en la dirección tangente a este plano.
Esta aceleración la sacamos de que la aceleración de una masa en un plano inclinado, sin rozamiento ni rodadura, es debida exclusivamente a la componente del peso paralela al plano (ya que la componente normal es compensada por la reacción del plano). Si tomamos como eje X el tangente al plano y hacia arriba, y como eje Y el normal al plano
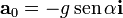
La aceleración de la gravedad, en este sistema de ejes, se escribe
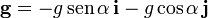
y la gravedad efectiva será
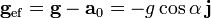
Esto quiere decir que la gravedad efectiva es perpendicular al plano inclinado, y por tanto al suelo del cajón. Esto quiere decir que un observador situado en el interior del cajón sin acceso al exterior, vería el péndulo colgando normalmente. Sin embargo, su periodo de oscilación aumenta, ya que la gravedad efectiva es menor que la real
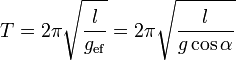
y la proporción entre este periodo y el no acelerado es
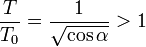
Para el caso 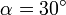 , este cociente vale 1.075, esto es, el reloj iría un 7.5% más lento.
, este cociente vale 1.075, esto es, el reloj iría un 7.5% más lento.






