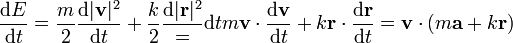Oscilador armónico bidimensional
De Laplace
(→Solución) |
(→Solución) |
||
| Línea 18: | Línea 18: | ||
y sus soluciones describirán curvas tridimensionales. | y sus soluciones describirán curvas tridimensionales. | ||
| + | |||
| + | En este problema tenemos una partícula situada en un plano. Su posición inicial está a una cierta distancia del punto de anclaje, en la dirección X. Esto quiere decir que el muelle inicialmente, tirará de la partícula con una fuerza en la dirección del eje X. Pero la partícula tiene una velocidad inicial paralela al eje Y. Esto quiere decir que, al menos al principio se moverá en la dirección de Y. Por tanto, necesariamente su movimiento será bidimensional. | ||
| + | |||
===Ley horaria=== | ===Ley horaria=== | ||
Para la partícula situada sobre la mesa, su movimiento será bidimensional y podrá describirse un sistema de coordenadas cartesiano | Para la partícula situada sobre la mesa, su movimiento será bidimensional y podrá describirse un sistema de coordenadas cartesiano | ||
| Línea 75: | Línea 78: | ||
===Constantes de movimiento=== | ===Constantes de movimiento=== | ||
| + | Se trata ahora de demostrar que la energía mecánica y el momento angular son constante de movimiento. Esto puede hacerse de diversas formas. | ||
| + | |||
| + | ====Energía mecánica==== | ||
| + | =====En forma vectorial===== | ||
| + | Como en el caso del [[Solución_general_del_MAS#Conservación_de_la_energía|oscilador armónico unidimensional]] podemos demostrar la constancia de la energía sin necesidad de conocer la solución. Aplicando que, para un vector dependiente del tiempo | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left|\mathbf{A}\right|^2 = \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\mathbf{A}\cdot\mathbf{A}\right) = 2\mathbd{A}\cdot\frac{\mathrm{d}\mathbf{A}}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | queda | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}E}{\mathrm{d}t} = \frac{m}{2}\frac{\mathrm{d}|\mathbf{v}|^2}{\mathrm{d}t}+\frac{k}{2}\frac{\mathrm{d}|\mathbf{r}|^2} = {\mathrm{d}t}m\mathbf{v}\cdot\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}+k\mathbf{r}\cdot\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t} = | ||
| + | \mathbf{v}\cdot\left(m\mathbf{a}+k\mathbf{r}\right)</math></center> | ||
| + | |||
| + | =====Como suma de dos energías===== | ||
[[Categoría:Problemas de movimiento oscilatorio]] | [[Categoría:Problemas de movimiento oscilatorio]] | ||
Revisión de 17:09 7 feb 2009
Contenido |
1 Enunciado
Una partícula de masa m se encuentra sobre una mesa, unida a un punto fijo de ésta (que tomaremos como origen de coordenadas) mediante un muelle de constante k. En el instante t = 0 se la sitúa en la posición 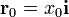 y se le comunica una velocidad
y se le comunica una velocidad 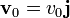 .
.
- Halle la posición de la partícula en cualquier instante.
- ¿Cómo es la trayectoria de la partícula?
- Demuestre que, en este movimiento, las cantidades
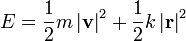
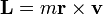
- son constantes de movimiento.
2 Solución
Aunque a la hora de pensar en osciladores armónicos, la visión más habitual es en términos de masas que se mueven en una sola dimensión, con un movimiento que varía sinusoidalmente en el tiempo, en realidad, un oscilador armónico no tiene por qué estar restringido a una sola dimension.
Lo que define al oscilador armónico, en general, es la ecuación de movimiento vectorial
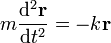
y sus soluciones describirán curvas tridimensionales.
En este problema tenemos una partícula situada en un plano. Su posición inicial está a una cierta distancia del punto de anclaje, en la dirección X. Esto quiere decir que el muelle inicialmente, tirará de la partícula con una fuerza en la dirección del eje X. Pero la partícula tiene una velocidad inicial paralela al eje Y. Esto quiere decir que, al menos al principio se moverá en la dirección de Y. Por tanto, necesariamente su movimiento será bidimensional.
2.1 Ley horaria
Para la partícula situada sobre la mesa, su movimiento será bidimensional y podrá describirse un sistema de coordenadas cartesiano
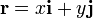
En este mismo sistema, la velocidad y la aceleración se escribirán
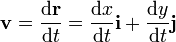
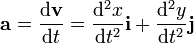
Sustituyendo en la ecuación de movimiento

y, puesto que dos vectores son iguales si lo son cada una de sus componentes, la ecuación vectorial se convierte en dos ecuaciones escalares
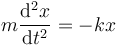
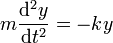
Esto quiere decir que el problema del oscilador armónico bidimensional (y el tridimensional) se puede reducir a dos osciladores armónicos unidimensionales (tres, en el tridimensional), cuya solución general es conocida:
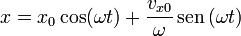

Combinando las dos soluciones obtenemos la solución general en forma vectorial
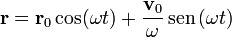
En nuestro caso, la posición inicial es


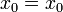
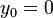
y la velocidad inicial



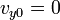
por lo que las ecuaciones horarias son
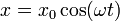
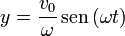
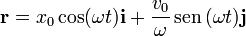
2.2 Trayectoria
La ley horaria nos proporciona unas ecuaciones paramétricas de la trayectoria
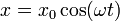
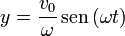
que podemos convertir en una ecuación implícita si eliminamos el tiempo entre ellas. Para ello, dividimos

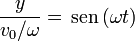
elevando al cuadrado y sumando
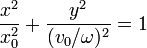
Esta es la ecuación de una elipse, con semiejes
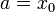
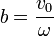
Así pues, aunque cada una de las dos coordenadas describe una sinusoide como función del tiempo, la combinación de ambos movimientos, teniendo en cuenta el desfase entre ellos (uno es un coseno y el otro un seno) da como resultado una elipse.
2.3 Constantes de movimiento
Se trata ahora de demostrar que la energía mecánica y el momento angular son constante de movimiento. Esto puede hacerse de diversas formas.
2.3.1 Energía mecánica
2.3.1.1 En forma vectorial
Como en el caso del oscilador armónico unidimensional podemos demostrar la constancia de la energía sin necesidad de conocer la solución. Aplicando que, para un vector dependiente del tiempo
queda