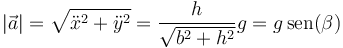Principio de D'Alembert (CMR)

De Laplace

(Diferencias entre revisiones)

Revisión de 18:39 7 ene 2016

Contenido

1 Introducción
2 Desplazamientos reales y virtuales
3 Vínculos ideales
4 Ecuación fundamental de la dinámica
5 Obtención de las ecuaciones de movimiento
6 Fuerzas de reacción vincular
7 Coordenadas generalizadas

1 Introducción

La formulación analítica de la dinámica es un planteamiento alternativo de las leyes de la mecánica empleando esencialmente cantidades relacionadas con la energía.

1.1 Notación

La Mecánica analítica trata principalmente con cantidades escalares. Por ello, aparecerán en las ecuaciones que siguen no tanto los vectores de posición de las partículas como sus coordenadas. Por ello, emplearemos la notación $x i$ para denotar cualquier coordenada cartesiana de las partículas del sistema. Si el sistema tiene una sola partícula, el indice i llegará hasta 3, si son dos hasta 6, etc. Para cada coordenada cartesiana se cumplirá la segunda ley de Newton

$m_i\ddot{x}_i=F_i\qquad\qquad i=1,2,\ldots 3N$

donde $m 1 = m 2 = m 3$ ya que se trata de las coordenadas de la misma partícula, pero eso no afecta a la validez de la expresión, y podemos hablar de la partícula i de manera individual.

Aquí $F i$ sería la componente de la fuerza sobre la partícula i según la dirección de la coordenada $x i$ .

1.2 Fuerzas

La fuerza sobre cada partícula será suma de las fuerzas aplicadas 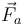$\vec{F}_a$ sobre la partícula y de las posibles fuerzas de reacción vincular, 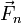$\vec{F}_n$ (donde usamos “n” por analogía con la fuerza normal de una superficie, pero como veremos no son necesariamente ortogonales)

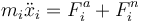
$m_i\ddot{x}_i=F^a_i+F^n_i$

Tanto las fuerzas aplicadas como las de reacción pueden ser tanto externas (como el peso o la reacción de una superficie rígida exterior al sistema) como internas (como las fuerzas eléctricas o la tensión de una varilla ideal que une dos partículas). A su vez, tanto unas como otras podrán ser funciones de las posiciones de las demás partículas, de sus velocidades y del tiempo.

$m_i\ddot{x}_i=F_i(x_k,\dot{x}_k,t)\qquad\qquad k=1,2,\ldots 3N$

1.3 Vínculo

Como sabemos, si existen r mvínculos, estas ecuaciones no son suficientes para determinar la evolución del sistema, ya que las fuerzas de reacción vincular son desconocidas a priori. Para completar el sistema se precisan las ecuaciones de los vínculos. Suponiendo solo vínculos bilaterales, tenemos los vínculos geométricos

$f_j(x_k,t)=0\qquad j = 1,\ldots r$

y los vínculos cinemáticos, de los que solo consideraremos los que son lineales en las velocidades

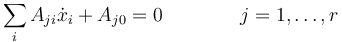
$\sum_i A_{ji}\dot{x}_i+A_{j0} = 0\qquad\qquad j = 1,\ldots,r$

donde los coeficientes $A j i$ son funciones de las coordenadas y el tiempo

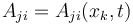
$A_{ji}=A_{ji}(x_k,t)\,$

Los vínculos geométricos también conducen a vínculos cinemáticos derivando respecto al tiempo. En ese caso

$A_{ji}=\frac{\partial f_j}{\partial x_i}\qquad\qquad A_{j0}=\frac{\partial f_i}{\partial t}$

Alternativamente, tenemos la forma pfaffiana de la ligadura, que relaciona los desplazamientos diferenciales

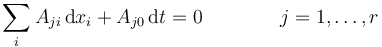
$\sum_i A_{ji}\,\mathrm{d}x_i+A_{j0}\,\mathrm{d}t = 0\qquad\qquad j = 1,\ldots,r$

1.4 Trabajo diferencial

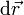Cuando una partícula sometida a una fuerza $\vec{F}$ realiza un desplazamiento diferencial $\mathrm{d}\vec{r}$ , el trabajo diferencial realizado por la fuerza se define como

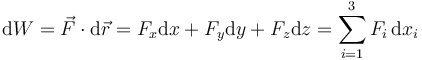
$\mathrm{d}W=\vec{F}\cdot\mathrm{d}\vec{r}=F_x\mathrm{d}x+F_y\mathrm{d}y+F_z\mathrm{d}z =\sum_{i=1}^3 F_i\,\mathrm{d}x_i$

Más en general, si tenemos un sistema sometido a diferentes fuerzas, el trabajo diferencial total será la suma de todos los trabajos individuales:

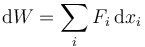
$\mathrm{d}W=\sum_i F_i\,\mathrm{d}x_i$

Si conocemos las fuerzas podemos hallar el trabajo, pero ¿qué ocurre cuando las fuerzas son desconocidas (como ocurre con las de reacción vincular), ¿a partir del trabajo podemos determinar las fuerzas? ¿Y el movimiento de la partícula? Veremos que, en un amplio abanico de casos sí es posible, al menos teóricamente.

La clave está en analizar cuándo es nulo ese trabajo. Si tenemos una única fuerza, de manera que el sumatorio se reduce a un solo término y sabemos que este trabajo es nulo cualquiera que sea el desplazamiento, la conclusión es que la fuerza debe ser nula

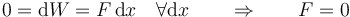
$0=\mathrm{d}W=F\,\mathrm{d}x\quad \forall \mathrm{d}x\qquad\Rightarrow\qquad F=0$

Si tenemos dos coordenadas y cada una puede variar independientemente, el razonamiento sigue siendo válido

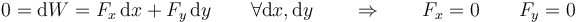
$0=\mathrm{d}W=F_x\,\mathrm{d}x+F_y\,\mathrm{d}y\qquad \forall \mathrm{d}x,\mathrm{d}y\qquad\Rightarrow\qquad F_x=0\qquad F_y=0$

Sin embargo, si existe un vínculo entre las coordenadas, el asunto se complica. Imaginemos que existe el vínculo de que la suma de las dos coordenadas es constante. En ese caso, lo que aumenta una es igual a lo que disminuye la otra. Las variaciones no son independientes

$x+y=A=\mathrm{cte.}\qquad\Rightarrow\qquad \mathrm{d}y=-\mathrm{d}x$

Llevando esto a la expresión del trabajo nulo

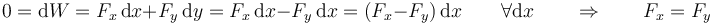
$0=\mathrm{d}W=F_x\,\mathrm{d}x+F_y\,\mathrm{d}y=F_x\,\mathrm{d}x-F_y\,\mathrm{d}x=(F_x-F_y)\,\mathrm{d}x\qquad \forall \mathrm{d}x\qquad\Rightarrow\qquad F_x=F_y$

es decir, podemos probar que las fuerzas serán iguales, pero no cuánto vale cada una. En las siguientes secciones precisaremos este resultado y veremos cómo se determinan las fuerzas y los movimientos.

2 Desplazamientos reales y virtuales

La primera distinción que debemos hacer es entre los denominados desplazamientos reales, posibles y virtuales.

Para ello comenzamos con el vínculo más simple posible: una partícula que se ve obligada a moverse sobre una superficie lisa estacionaria

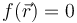
$f(\vec{r})=0$

Este vínculo es bilateral, esclerónomo, liso y holónomo. En su forma pfaffiana, escribiremos este vínculo como una relación entre los diferenciales

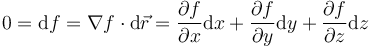
$0 = \mathrm{d}f=\nabla f\cdot\mathrm{d}\vec{r}=\frac{\partial f}{\partial x}\mathrm{d}x+\frac{\partial f}{\partial y}\mathrm{d}y+\frac{\partial f}{\partial z}\mathrm{d}z$

Puesto que el desplamiento debe ser forzosamente tangente a la superficie, esta relación implica que el vector gradiente es perpendicular a ella.

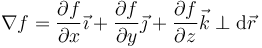
$\nabla f = \frac{\partial f}{\partial x}\vec{\imath}+\frac{\partial f}{\partial y}\vec{\jmath}+\frac{\partial f}{\partial z}\vec{k}\perp \mathrm{d}\vec{r}$

Si el vínculo es liso, la fuerza de reacción vincular es también perpendicular a la superficie (proporcional, por tanto, al gradiente) y por ello no realiza trabajo en el desplazamiento

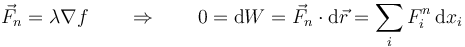
$\vec{F}_n=\lambda \nabla f \qquad\Rightarrow\qquad 0=\mathrm{d}W=\vec{F}_n\cdot\mathrm{d}\vec{r}=\sum_i F^n_i\,\mathrm{d}x_i$

Por tanto, para este tipo de vínculos el trabajo realizado por la fuerza de reacción vincular es nulo. Este resultado vale tanto para el desplazamiento real que realiza la partícula, como para todos los desplazamientos posibles compatibles con la ligadura.

Sin embargo, esto no siempre es cierto. Consideremos el caso de una partícula en el suelo liso de un ascensor que asciende. En este caso, no es cierto que la fuerza sea ortogonal al desplazamiento, ya que éste posee una componente en la dirección vertical, que es la misma de la fuerza. Es más, si el ascensor sube una altura $h$ , la partícula gana una energía potencial $m g h$ . ¿De donde ha salido esta energía? Del trabajo realizado por la fuerza de reacción, que es la que está moviendo a la partícula en contra del peso. Por tanto, no solo es que el trabajo no sea nulo, es que puede ser crucial en los cálculos.

Precisando, si el vínculo es de la forma

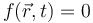
$f(\vec{r},t)=0$

su forma pfaffiana será

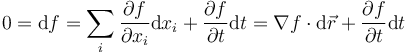
$0 = \mathrm{d}f = \sum_i\frac{\partial f}{\partial x_i}\mathrm{d}x_i+\frac{\partial f}{\partial t}\mathrm{d}t=\nabla f\cdot\mathrm{d}\vec{r}+\frac{\partial f}{\partial t}\mathrm{d}t$

La fuerza de reacción vincular sigue siendo perpendicular a la superficie en cada instante

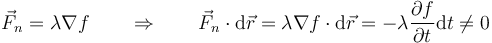
$\vec{F}_n=\lambda \nabla f\qquad\Rightarrow\qquad \vec{F}_n\cdot\mathrm{d}\vec{r}=\lambda\nabla f \cdot\mathrm{d}\vec{r}=-\lambda\frac{\partial f}{\partial t}\mathrm{d}t\neq 0$

Vemos que la diferencia se debe a la derivada temporal del vínculo.

Definimos entonces los desplazamientos virtuales, $δ x i$ , como aquellos que son compatibles con el vínculo, suponiendo éste congelado en el tiempo, es decir, que cumplen la relación

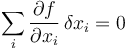
$\sum_i \frac{\partial f}{\partial x_i}\,\delta x_i = 0$

Obsérvese que la definición del desplazamiento virtual es sutil, ya que el tiempo sigue apareciendo en la expresión (está dentro de las derivadas parciales). Lo que hacemos es tratarlo como un parámetro, no como una variable. Por hacer una analogía, un vínculo que fuera el movimiento restringido a la superficie de un globo de aire caliente dependerá de la temperatura del aire, pero esa temperatura es un parámetro que nos da el tamaño del globo, no una coordenada. Aquí estaríamos tratando el tiempo de la misma forma.

Más en general, si un vínculo es de la forma pfaffiana

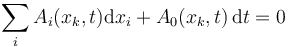
$\sum_i A_{i}(x_k,t)\mathrm{d}x_i+A_0(x_k,t)\,\mathrm{d}t=0$

se dice que un desplazamiento virtual que satisface este vínculo es el que verifica

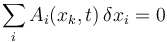
$\sum_i A_{i}(x_k,t)\,\delta x_i=0$

Tenemos entonces tres tipos de desplazamientos diferenciales:

Reales, $d x i$: son los que de hecho efectúan las partículas del sistema, sometidas a las fuerzas de reacción vincular y a las fuerzas aplicadas. En cada problema concreto y en cada instante habrá un único desplazamiento real.
Posibles, $d x i$: son aquellos compatibles con todas las ecuaciones de los vínculos, sin considerar las fuerzas aplicadas. En cada problema y en cada instante habrá una infinitud de desplazamientos posibles. Estos desplazamientos forman un espacio afín de dimensión GDL = 3N-r (el número de grados de libertad). Todo desplazamiento real es un desplazamiento posible.
Virtuales, $δ x i$: son los compatibles con los vínculos suponiendo estos independientes del tiempo en cada instante. Otra forma de definirlos es decir que la diferencia entre dos desplazamientos posibles es un desplazamiento virtual. Los desplazamientos virtuales forman un espacio vectorial de dimensión GDL = 3N-r. En general, un desplazamiento real no coincidirá con uno virtual.

Esta clasificación permite una clasificación adicional de las ligaduras: un vínculo es catastático cuando los desplazamientos virtuales coinciden con los desplazamientos posibles, es decir, es de la forma

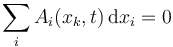
$\sum_i A_i(x_k,t)\,\mathrm{d}x_i = 0$

Los vínculos esclerónomos son catastáticos, pero también existen otros vínculos no holónomos que satisfacen esta relación aunque dependan del tiempo.

Si no es catastático, se dice que es acatastático. Los vínculos geométricos reónomos son acatastáticos.

3 Vínculos ideales

Hemos visto que la fuerza de reacción vincular debida a una superficie lisa es perpendicular a ésta. Por tanto su trabajo en un desplamiento virtual (lo que se conoce como trabajo virtual) es nulo

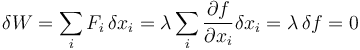
$\delta W = \sum_i F_i\,\delta x_i = \lambda \sum_i \frac{\partial f}{\partial x_i}\delta x_i = \lambda\,\delta f = 0$

Nótese que no se anula cada uno de los sumandos por separado. Lo que se anula es la suma.

Existen más fuerzas de reacción vincular que verifican esta relación, aunque no sean ortogonales a una superficie material.

Tensión en un hilo: Así, en el caso de dos masas unidas por un hilo que pasa por una polea ideal, la fuerza de reacción es la tensión del hilo. Esta tensión va en la misma dirección en que se desplazan las masas, por lo que su trabajo obviamente no es nulo. No obstante, sí se cumple que la tensión del hilo, si es ideal, es la misma para las dos masas, mientras que los desplazamientos virtuales son opuestos

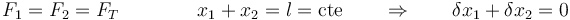
$F_1 = F_2 = F_T\qquad\qquad x_1+x_2 = l=\mathrm{cte}\qquad\Rightarrow\qquad \delta x_1+\delta x_2=0$

Por ello, se anula el trabajo virtual total

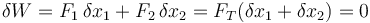
$\delta W = F_1\,\delta x_1 + F_2\,\delta x_2 =F_T(\delta x_1+\delta x_2)=0$

Fuerzas en un sólido rígido: De la misma manera se anula el trabajo virtual debido a las fuerzas entre dos partículas que satisfacen la condición de rigidez, es decir, que la distancia entre ellas permanece constante. Si las partículas están en los puntos A y B, sus velocidades cumplen

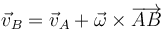
$\vec{v}_B=\vec{v}_A+\vec{\omega}\times \overrightarrow{AB}$

Multiplicando por el diferencial de tiempo queda la relación entre desplazamientos

$\delta\vec{r}_B=\delta\vec{r}_A+\delta\theta\vec{u}\times\overrightarrow{AB}$

siendo

δθ

el ángulo diferencial girado en torno al eje marcado por $\vec{u}$ . Llevando esto a la expresión del trabajo virtual total

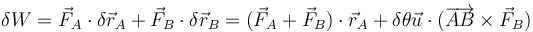
$\delta W= \vec{F}_A\cdot\delta\vec{r}_A+\vec{F}_B\cdot\delta\vec{r}_B = (\vec{F}_A+\vec{F}_B)\cdot\vec{r}_A+\delta\theta\vec{u}\cdot(\overrightarrow{AB}\times\vec{F}_{B})$

Por la tercera ley de Newton, se anula el primer sumando (porque las fuerzas son opuestas) y el segundo (porque son paralelas a la línea que une las partículas). Por tanto, el trabajo virtual debido a estas fuerzas es nulo.

Rozamiento estático: En el caso de un cuerpo sólido apoyado sobre otro de forma que existe una fuerza de rozamiento estático entre ellos, las fuerzas de reacción vincular si son tangentes a la superficie de contacto (a diferencia de los vínculos lisos), pero ahora lo que se anulan son los desplzamientos virtuales, ya que el vínculo es que la posición relativa permanezca inmóvil. Por tanto, también se anula el trabajo virtual.

Este tipo de fuerzas de reacción incluye el caso importante de la rodadura sin deslizamiento entre sólidos.

Como vemos, el conjunto de situaciones en que se anula el trabajo virtual de las fuerzas de reacción es bastante amplio.

Definimos entonces los vínculos ideales como aquellos cuyas fuerzas de reacción vincular producen un trabajo nulo ante desplazamientos virtuales

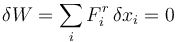
$\delta W = \sum_i F^r_i\, \delta x_i = 0$

siendo los $δ x i$ los compatibles con todos los vínculos presentes

$\sum_i A_{ji}\delta x_i = 0\qquad\qquad j = 1,\ldots, r$

La excepción más importante en la que no se anula el trabajo virtual es el caso del rozamiento dinámico. En este caso, sí hay fuerzas y desplazamientos tangentes a las superficies de contacto, por lo que el trabajo virtual es no nulo. Lo que se hace en estos casos es tratar la fuerza de rozamiento dinámico no como una de reacción, sino como una fuerza aplicada. Para que esto sea factible, debemos disponer de alguna ley física para el rozamiento, como puede ser la ley de Coulomb del rozamiento seco. De manera similar se tratan otras fuerzas no conservativas como pueden ser las ejercidas por un motor.

4 Ecuación fundamental de la dinámica

Hemos visto que los sistemas sometidos a fuerzas de reacción vincular, que son incógnitas adicionales de los problemas, satisfacen en numerosas ocasiones que no realizan trabajo en un desplazamiento virtual.

Se trata ahora de darle la vuelta al razonamiento y partiendo de este hecho, conseguir varios objetivos:

Eliminar las fuerzas de reacción de los problemas, y trabajar solo con las fuerzas aplicadas.
Determinar el movimiento el sistema.
Calcular a posteriori las fuerzas de reacción.

Para ello, suponemos un sistema descrito por 3N coordenadas cartesianas, cada una de las cuales satisface la segunda ley de Newton

$m_i \ddot{x}_i=F^a_i+F^n_i\qquad\qquad i=1,\ldots,3N$

Admitimos que las fuerzas de reacción vincular son ideales, es decir, no realizan trabajo en un desplazamiento virtual. En ese caso podemos hacer

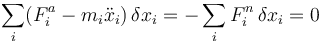
$\sum_i(F^a_i-m_i\ddot{x}_i)\,\delta x_i = -\sum_i F^n_i\,\delta x_i = 0$

es decir, la suma de las fuerzas activas y los términos inerciales cambiados de signo tampoco realizan trabajo virtual. Esta es la ecuación fundamental de la dinámica o Principio de D'Alembert

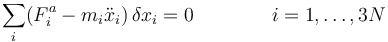
$\sum_i(F^a_i-m_i\ddot{x}_i)\,\delta x_i = 0\qquad\qquad i = 1,\ldots,3N$

donde los desplazamientos virtuales están relacionados por r ecuaciones de vínculo

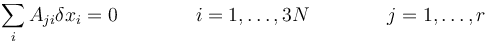
$\sum_{i}A_{ji}\delta x_i = 0 \qquad\qquad i=1,\ldots,3N\qquad\qquad j=1,\ldots,r$

Si agrupamos las coordenadas cartesianas en los vectores de posición de las diferentes partículas queda la relación vectorial

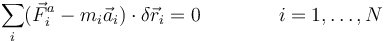
$\sum_i (\vec{F}^a_i-m_i\vec{a}_i)\cdot\delta\vec{r}_i = 0\qquad\qquad i=1,\ldots,N$

En el caso estático todas las aceleraciones son nulas y la ecuación se reduce a una relación entre las fuerzas aplicadas, conocida como Principio de los trabajos virtuales

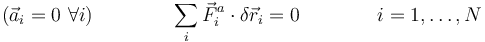
$(\vec{a}_i=0\ \forall i)\qquad\qquad\sum_i \vec{F}^a_i\cdot\delta\vec{r}_i = 0\qquad\qquad i=1,\ldots,N$

El principio de D'Alembert puede entenderse como una generalización del principio de los trabajos virtuales si consideramos que sobre cada partícula actúa una fuerza de inercia 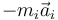$-m_i\vec{a}_i$ .

La ecuación fundamental de la dinámica es una única ecuación escalar. ¿Cómo pueden obtenerse a partir de ella las ecuaciones de movimiento para todas las coordenadas?

5 Obtención de las ecuaciones de movimiento

La clave es que debe cumplirse para cualquier desplazamiento virtual compatible con las ligaduras. Si un $δ x i$ puede tomar cualquier valor (infinitesimal) entonces su coeficiente debe anularse para que la suma total sea nula en todo caso.

Los desplazamiento de las diferentes coordenadas no son todos independientes entre sí, ya que están relacionados por los r vínculos. Las ecuaciones de los vínculos constituyen un sistema de r ecuaciones con 3N incógnitas. Podemos despejar de ellas r desplazamientos en función de los restantes 3N-r y sustituir en la ecuación fundamental de la dinámica. De esta forma, en esta ecuación aparecerán solo 3N-r diferenciales independientes, lo que permite anular cada coeficiente y obtener 3N-r ecuaciones.

No acaba ahí el proceso, ya que aunque de una sola ecuación hemos obtenido 3N-r ecuaciones distintas, tantas como grados de libertad del sistema, éstas siguen incluyendo 3N variables. Por tanto, hay que suplementar el sistema con las r ecuaciones de vínculo para llegar a 3N ecuaciones con 3N incógnitas.

Hay que destacar que todo este procedimiento no garantiza que resulten ecuaciones simples o que puedan siquiera despejarse unas variables en función de otras para ir sustituyendo sucesivamente.

Máquina de Atwood

Como ejemplo simple, consideremos dos masas $m 1$ y $m 2$ unidas por un hilo que pasa por una polea ideal (sin masa y sin rozamiento), de forma que ambas cuelgan verticalmente. ¿Cuánto vale la aceleración con la que se mueven las masas?

Si consideramos el eje X vertical y hacia abajo, la ecuación fundamental de la dinámica puede escribirse como

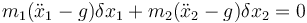
$m_1(\ddot{x}_1-g)\delta x_1+m_2(\ddot{x}_2-g)\delta x_2 = 0$

Las coordenadas están relacionadas por el vínculo

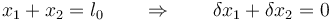
$x_1+x_2 = l_0\qquad\Rightarrow\qquad \delta x_1 + \delta x_2 = 0$

lo que llevado a la ecuación anterior nos da

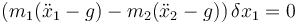
$\left(m_1(\ddot{x}_1-g)-m_2(\ddot{x}_2-g)\right)\delta x_1=0$

Como $δ x 1$ es arbitrario, el coeficiente debe anularse:

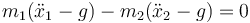
$m_1(\ddot{x}_1-g)-m_2(\ddot{x}_2-g)=0$

Por otro lado, del mismo vínculo tenemos

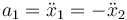
$a_1 = \ddot{x}_1=-\ddot{x}_2$

y por tanto

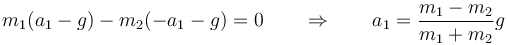
$m_1(a_1-g)-m_2(-a_1-g)=0\qquad\Rightarrow\qquad a_1= \frac{m_1-m_2}{m_1+m_2}g$

El plano inclinado

Consideremos ahora el caso de una partícula que desciende sin rozamiento por un plano inclinado de base $b$ y altura $h$ . ¿Cuánto vale su aceleración?

Tomamos un sistema de ejes en el que el Y es el vertical hacia arriba y el X es horizontal.

La ecuación fundamental se lee ahora

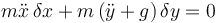
$m\ddot{x}\,\delta x+m\left(\ddot{y}+g\right)\delta y = 0$

siendo la ecuación del vínculo

$\frac{x}{b}+\frac{y}{h}=1\qquad\Rightarrow\qquad \frac{\delta x}{b}+\frac{\delta y}{h}=0$

Despejamos y sustituimos, llegando a

$-\frac{b}{h}\ddot{x}+\ddot{y}-g=0$

Como además, por la misma ecuación del vínculo,

$\ddot{x}=-\frac{b}{h}\ddot{y}$

llegamos a

$\ddot{y}= -\frac{h^2}{h^2+b^2}g\qquad\qquad \ddot{x}=\frac{bh}{h^2+b^2}g$

Este puede no parecer el conocido resultado del plano inclinado, pero si hallamos el módulo de esta aceleración queda

$\left|\vec{a}\right|=\sqrt{\ddot{x}^2+\ddot{y}^2}=\frac{h}{\sqrt{b^2+h^2}}g=g\,\mathrm{sen}(\beta)$

6 Fuerzas de reacción vincular

7 Coordenadas generalizadas

@@ Línea 214: / Línea 214: @@
 <center><math>(\vec{a}_i=0\ \forall i)\qquad\qquad\sum_i \vec{F}^a_i\cdot\delta\vec{r}_i = 0\qquad\qquad i=1,\ldots,N</math></center>
-El principio de D'Alembert puede entenderse como una generalización del principio de los trabajos virtuales si consideramos que sobre cada partícula actúa una fuerza de inercia <math>-m_i\vec{a}_i</math>
+El principio de D'Alembert puede entenderse como una generalización del principio de los trabajos virtuales si consideramos que sobre cada partícula actúa una fuerza de inercia <math>-m_i\vec{a}_i</math>.
+La ecuación fundamental de la dinámica es una única ecuación escalar. ¿Cómo pueden obtenerse a partir de ella las ecuaciones de movimiento para todas las coordenadas?
+==Obtención de las ecuaciones de movimiento==
+La clave es que debe cumplirse para cualquier desplazamiento virtual compatible con las ligaduras. Si un <math>\delta x_i</math> puede tomar cualquier valor (infinitesimal) entonces su coeficiente debe anularse para que la suma total sea nula en todo caso.
+Los desplazamiento de las diferentes coordenadas no son todos independientes entre sí, ya que están relacionados por los r vínculos. Las ecuaciones de los vínculos constituyen un sistema de r ecuaciones con 3N incógnitas. Podemos despejar de ellas r desplazamientos en función de los restantes 3N-r y sustituir en la ecuación fundamental de la dinámica. De esta forma, en esta ecuación aparecerán solo 3N-r diferenciales independientes, lo que permite anular cada coeficiente y obtener 3N-r ecuaciones.
+No acaba ahí el proceso, ya que aunque de una sola ecuación hemos obtenido 3N-r ecuaciones distintas, tantas como grados de libertad del sistema, éstas siguen incluyendo 3N variables. Por tanto, hay que suplementar el sistema con las r ecuaciones de vínculo para llegar a 3N ecuaciones con 3N incógnitas.
+Hay que destacar que todo este procedimiento no garantiza que resulten ecuaciones simples o que puedan siquiera despejarse unas variables en función de otras para ir sustituyendo sucesivamente.
+{{ejemplo|'''Máquina de Atwood'''
+Como ejemplo simple, consideremos dos masas <math>m_1</math> y <math>m_2</math> unidas por un hilo que pasa por una polea ideal (sin masa y sin rozamiento), de forma que ambas cuelgan verticalmente. ¿Cuánto vale la aceleración con la que se mueven las masas?
+Si consideramos el eje X vertical y hacia abajo, la ecuación fundamental de la dinámica puede escribirse como
+<center><math>m_1(\ddot{x}_1-g)\delta x_1+m_2(\ddot{x}_2-g)\delta x_2 = 0</math></center>
+Las coordenadas están relacionadas por el vínculo
+<center><math>x_1+x_2 = l_0\qquad\Rightarrow\qquad \delta x_1 + \delta x_2 = 0</math></center>
+lo que llevado a la ecuación anterior nos da
+<center><math>\left(m_1(\ddot{x}_1-g)-m_2(\ddot{x}_2-g)\right)\delta x_1=0</math></center>
+Como <math>\delta x_1</math> es arbitrario, el coeficiente debe anularse:
+<center><math>m_1(\ddot{x}_1-g)-m_2(\ddot{x}_2-g)=0</math></center>
+Por otro lado, del mismo vínculo tenemos
+<center><math>a_1 = \ddot{x}_1=-\ddot{x}_2</math></center>
+y por tanto
+<center><math>m_1(a_1-g)-m_2(-a_1-g)=0\qquad\Rightarrow\qquad a_1= \frac{m_1-m_2}{m_1+m_2}g</math></center>
+}}
+&nbsp;
+{{ejemplo|'''El plano inclinado'''
+Consideremos ahora el caso de una partícula que desciende sin rozamiento por un plano inclinado de base <math>b</math> y altura <math>h</math>. ¿Cuánto vale su aceleración?
+Tomamos un sistema de ejes en el que el Y es el vertical hacia arriba y el X es horizontal.
+La ecuación fundamental se lee ahora
+<center><math>m\ddot{x}\,\delta x+m\left(\ddot{y}+g\right)\delta y = 0</math></center>
+siendo la ecuación del vínculo
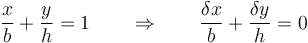
+<center><math>\frac{x}{b}+\frac{y}{h}=1\qquad\Rightarrow\qquad \frac{\delta x}{b}+\frac{\delta y}{h}=0</math></center>
+Despejamos y sustituimos, llegando a
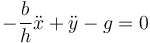
+<center><math>-\frac{b}{h}\ddot{x}+\ddot{y}-g=0</math></center>
+Como además, por la misma ecuación del vínculo,
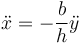
+<center><math>\ddot{x}=-\frac{b}{h}\ddot{y}</math></center>
+llegamos a
+<center><math>\ddot{y}= -\frac{h^2}{h^2+b^2}g\qquad\qquad \ddot{x}=\frac{bh}{h^2+b^2}g</math></center>
+Este puede no parecer el conocido resultado del plano inclinado, pero si hallamos el módulo de esta aceleración queda
+<center><math>\left|\vec{a}\right|=\sqrt{\ddot{x}^2+\ddot{y}^2}=\frac{h}{\sqrt{b^2+h^2}}g=g\,\mathrm{sen}(\beta)</math></center>
+}}
 ==Fuerzas de reacción vincular==
 ==Coordenadas generalizadas==
 [[Categoría:Mecánica analítica (CMR)]]

Principio de D'Alembert (CMR)

De Laplace

Revisión de 18:39 7 ene 2016

Contenido

1 Introducción

1.1 Notación

1.2 Fuerzas

1.3 Vínculo

1.4 Trabajo diferencial

2 Desplazamientos reales y virtuales

3 Vínculos ideales

4 Ecuación fundamental de la dinámica

5 Obtención de las ecuaciones de movimiento

6 Fuerzas de reacción vincular

7 Coordenadas generalizadas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES