Problemas de Dinámica Analítica (MR G.I.C.)
De Laplace
(→Engranaje sobre cremallera) |
(→Engranaje sobre cremallera) |
||
| Línea 4: | Línea 4: | ||
#Encuentra el número de grados de libertad y elige un conjunto de coordenadas generalizadas para describir el movimiento. | #Encuentra el número de grados de libertad y elige un conjunto de coordenadas generalizadas para describir el movimiento. | ||
#Encuentra las ecuaciones diferenciales del movimiento. | #Encuentra las ecuaciones diferenciales del movimiento. | ||
| + | |||
| + | ==[[Deslizadera y disco rodando sin deslizar (MR G.I.C.) | Deslizadera y disco rodando sin deslizar]]== | ||
| + | [[File:MR_disco_deslizadera_enunciado.png|right]] | ||
| + | Un disco homogéneo (sólido "2") de masa <math>m</math> y radio <math>R</math> puede rotar alrededor de su | ||
| + | centro <math>C</math>, que se mantiene fijo. Una deslizadera vertical (sólido "0"), de masa <math>m</math> | ||
| + | puede moverse a lo largo del | ||
| + | eje <math>O_1Y_1</math>, de modo que en el punto de contacto <math>A</math> el disco rueda sin deslizar sobre el | ||
| + | sólido "0". La deslizadera está conectada a un muelle de constante elástica <math>k</math> y | ||
| + | longitud natural <math>l_0</math>. El otro extremo del muelle está anclado en un punto fijo del eje | ||
| + | <math>O_1X_1</math>, de modo que se mantiene siempre vertical. El sistema está sometido a la acción de la gravedad como se indica en la figura. | ||
| + | |||
| + | #¿Cuantos grados de libertad tiene el sistema? Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21}, así como sus derivadas temporales. El resultado debe quedar en función del número de grados de libertad y sus derivadas temporales. | ||
| + | #Calcula las energías cinética y potencial del sistema en función de sus grados de libertad. | ||
| + | #Escribe la lagrangiana del sistema, así como las ecuaciones diferenciales de movimiento. | ||
| + | #Se aplica sobre el disco un par de fuerzas externo <math>\vec{\tau} = \tau_0\cos(\omega t)\,\vec{k}_1</math>. Encuentra las ecuaciones de movimiento en este caso. ¿Para qué valor de <math>\omega</math> aparece una resonancia mecánica? | ||
| + | #Ahora no hay par aplicado. Se aplica una percusión <math>\vec{\hat{F}}=[\hat{F}_0, \hat{F}_0,0]_1</math> sobre el punto <math>B</math> del sólido "2". En el instante de la percusión se cumple <math>s(0)=l_0</math>, <math>\theta(0)=0</math>, <math>\dot{s}(0^-)=0</math>, <math>\dot{\theta}(0^-)=0</math>. Calcula el estado del sistema inmediatamente después de la percusión. | ||
Revisión de 17:07 25 sep 2017
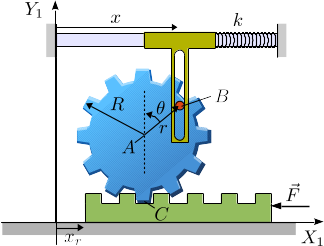
1 Engranaje sobre cremallera
La figura muestra un sistema mecánico formado por un engranaje que rueda sobre una cremallera y está conectado a un deslizador con una ranura que desliza respecto al pasador en B. El deslizador está acoplado a un muelle, de constante elástica k, que se encuentra relajado cuando x = 2R. En ese instante se tiene θ = 0. Las masas del engranaje, el deslizador y la cremallera son la misma e igual a m. El radio de giro del engranaje es rc. El contacto entre el pasador y la ranura es liso. El mecanismo es accionado por una fuerza aplicada sobe la cremallera como se indica en la figura.
- Encuentra el número de grados de libertad y elige un conjunto de coordenadas generalizadas para describir el movimiento.
- Encuentra las ecuaciones diferenciales del movimiento.
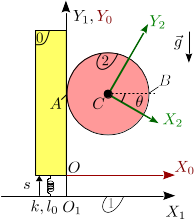
2 Deslizadera y disco rodando sin deslizar
Un disco homogéneo (sólido "2") de masa m y radio R puede rotar alrededor de su centro C, que se mantiene fijo. Una deslizadera vertical (sólido "0"), de masa m puede moverse a lo largo del eje O1Y1, de modo que en el punto de contacto A el disco rueda sin deslizar sobre el sólido "0". La deslizadera está conectada a un muelle de constante elástica k y longitud natural l0. El otro extremo del muelle está anclado en un punto fijo del eje O1X1, de modo que se mantiene siempre vertical. El sistema está sometido a la acción de la gravedad como se indica en la figura.
- ¿Cuantos grados de libertad tiene el sistema? Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21}, así como sus derivadas temporales. El resultado debe quedar en función del número de grados de libertad y sus derivadas temporales.
- Calcula las energías cinética y potencial del sistema en función de sus grados de libertad.
- Escribe la lagrangiana del sistema, así como las ecuaciones diferenciales de movimiento.
- Se aplica sobre el disco un par de fuerzas externo
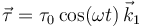. Encuentra las ecuaciones de movimiento en este caso. ¿Para qué valor de ω aparece una resonancia mecánica?
- Ahora no hay par aplicado. Se aplica una percusión
![\vec{\hat{F}}=[\hat{F}_0, \hat{F}_0,0]_1](/wiki/images/math/a/0/d/a0d931a1104a4fbfcf8b201fe4dc7018.png)
sobre el punto B del sólido "2". En el instante de la percusión se cumple s(0) = l0, θ(0) = 0,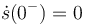 
, 
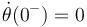. Calcula el estado del sistema inmediatamente después de la percusión.
