Solución general del MAS

De Laplace

(Diferencias entre revisiones)

Revisión de 12:32 7 feb 2009

Contenido

1 Enunciado
2 Solución

1 Enunciado

La solución general de la ecuación de movimiento

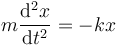
$m\frac{\mathrm{d}^2x}{\mathrm{d}t^2} = -k x$

es de la forma

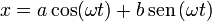
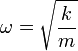
$x = a \cos(\omega t)+b\,\mathrm{sen}\,(\omega t)$ $\omega=\sqrt{\frac{k}{m}}$

con $a$ y $b$ dos constantes dependientes de las condiciones iniciales.

Halle el valor de las constantes $a$ y $b$ si la posición inicial de la partícula es $x 0$ y su velocidad inicial es $v 0$ .
Calcule la velocidad de la partícula para cualquier instante en función de la posición y velocidad iniciales.
Demuestre que la ecuación horaria 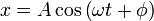$x = A \cos\left(\omega t+\phi\right)$ es también solución de la misma ecuación de movimiento. Empleando relaciones trigonométricas, deduzca la relación entre las constantes ${A,φ}$ y las constantes ${a, b}$ . Exprese $A$ y $φ$ en función de la posición y la velocidad iniciales, $x 0$ y $v 0$ .
Demuestre que la cantidad $E = m v 2 / 2 + k x 2 / 2$ no depende del tiempo. ¿Cuánto vale en función de las condiciones iniciales?
Demuestre que $x = e jω t$ , con 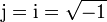$\mathrm{j}=\mathrm{i}=\sqrt{-1}$ , la unidad imaginaria, es una solución particular de la ecuación de movimiento. Aplicando los resultados anteriores, demuestre la relación

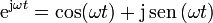
$\mathrm{e}^{\mathrm{j}\omega t}=\cos(\omega t)+\mathrm{j}\,\mathrm{sen}\,(\omega t)$

2 Solución

2.1 Valor de a y b

Haciendo $t = 0$ en la ley horaria, el resultado debe ser igual a la posición inicial

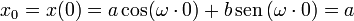
$x_0 = x(0) = a \cos(\omega\cdot 0) + b\,\mathrm{sen}\,(\omega\cdot 0) = a$ $\Rightarrow$ $a = x_0\,$

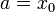
Para hallar $b$ necesitamos la velocidad. Derivando en la ley horaria

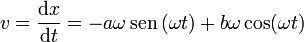
$v = \frac{\mathrm{d}x}{\mathrm{d}t}= -a\omega\,\mathrm{sen}\,(\omega t)+b\omega\cos(\omega t)$

y su valor en $t = 0$ nos da $b$

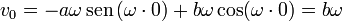
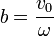
$v_0 = -a\omega\,\mathrm{sen}\,(\omega\cdot 0)+b\omega\cos(\omega\cdot 0) = b\omega$ $\Rightarrow$ $b = \frac{v_0}{\omega}$

Por tanto, la posición en cualquier instante, en función de las condiciones iniciales, es

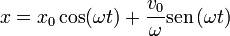
$x = x_0\cos(\omega t)+\frac{v_0}{\omega}\mathrm{sen}\,(\omega t)$

Como casos particulares tenemos

el de una partícula que se libera desde una cierta posición en reposo

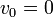
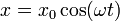
$v_0 = 0\,$ $x= x_0\cos(\omega t)\,$

el de una partícula a la que se comunica un impulso inicial en la posición de equilibrio

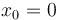
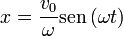
$x_0 = 0\,$ $x= \frac{v_0}{\omega}\mathrm{sen}\,(\omega t)$

2.2 Velocidad

Conocida la posición en función de las condiciones iniciales, el cálculo de la velocidad en cada instante es inmediato:

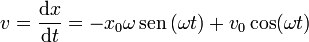
$v = \frac{\mathrm{d}x}{\mathrm{d}t} = -x_0\omega\,\mathrm{sen}\,(\omega t)+v_0\cos(\omega t)$

Para los casos particulares anteriores:

Una partícula que se libera desde una cierta posición en reposo

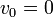
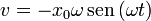
$v_0 = 0\,$ $v= -x_0\omega\,\mathrm{sen}\,(\omega t)$

el de una partícula a la que se comunica un impulso inicial en la posición de equilibrio

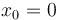
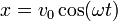
$x_0 = 0\,$ $x= v_0\cos(\omega t)\,$

2.3 Amplitud y desfase

Una manera alternativa de escribir la solución general es en la forma

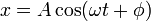
$x = A \cos(\omega t+\phi)\,$

donde $A$ es la amplitud del movimiento y $\phi\,$ es su desfase.

Veamos en primer lugar que se trata de una solución de la ecuación de movimiento. Derivando dos veces

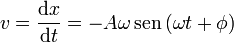
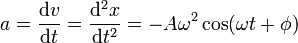
$v = \frac{\mathrm{d}x}{\mathrm{d}t}= -A\omega\,\mathrm{sen}\,(\omega t+\phi)$ $a = \frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}^2x}{\mathrm{d}t^2}=-A\omega^2\cos(\omega t+\phi)$

y sustituyendo

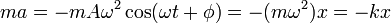
$ma = -mA\omega^2\cos(\omega t+\phi) = -(m\omega^2)x = - kx\,$

Por tanto, es una solución de la ecuación de movimiento. Queda por ver que se trata de una solución general.

Dado que la solución general de la ecuación de movimiento puede escribirse en la forma indicada en el enunciado, la que acabamos de comprobar también podrá escribirse en la misma forma, esto es, existen dos constantes $a$ y $b$ tales que

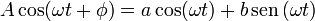
$A\cos(\omega t+\phi) = a\cos(\omega t)+b\,\mathrm{sen}\,(\omega t)$

Para hallar sus valores, aplicamos la relación trigonométrica

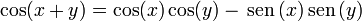
$\cos(x+y) = \cos(x)\cos(y)-\,\mathrm{sen}\,(x)\,\mathrm{sen}\,(y)$

que, aplicada a nuestro caso, da

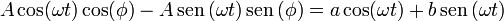
$A\cos(\omega t)\cos(\phi) - A\,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(\phi)= a\cos(\omega t)+b\,\mathrm{sen}\,(\omega t)$

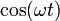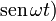Puesto que $a$ y $b$ deben ser independientes del tiempo, y esta relación debe cumplirse en todo instante, los coeficientes de $\cos(\omega t)\,$ y $\mathrm{sen}\,\omega t)$ de un miembro deben ser iguales a los del otro miembro:

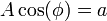
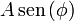
$A\cos(\phi) = a\,$ $A\,\mathrm{sen}\,(\phi)$

o, equivalentemente

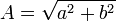
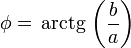
$A = \sqrt{a^2+b^2}$ $\phi = \,\mathrm{arctg}\,\left(\frac{b}{a}\right)$

Estas relaciones, y las anteriores, permiten calcular $A$ y $\phi\,$ , dados a y b arbitrarios, y viceversa. Esto quiere decir que la solución en términos de la amplitud y el desfase no es solamente una solución particular, sino una general.

Gráficamente, el paso de las constantes ${a, b}$ a las constantes ${A,φ}$ equivale a un paso de cartesianas a polares, siendo $A$ el módulo y $\phi\,$ el ángulo.

En términos de las condiciones iniciales

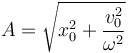
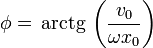
$A = \sqrt{x_0^2+\frac{v_0^2}{\omega^2}}$ $\phi = \,\mathrm{arctg}\,\left(\frac{v_0}{\omega x_0}\right)$

2.4 Conservación de la energía

Existen varias formas de demostrar la conservación de la energía mecánica

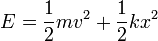
$E = \frac{1}{2}mv^2+\frac{1}{2}kx^2$

2.4.1 Derivada temporal

La forma más general de demostrar que una cantidad es una constante de movimiento (o integral primera) es probando que su derivada respecto al tiempo se anula.

En nuestro caso, $m$ y $k$ son constantes del problema, pero $x$ y $v$ son funciones del tiempo, así que la derivada de la energía, aplicando dos veces que

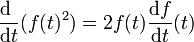
$\frac{\mathrm{d}\ }{\mathrm{d}t}(f(t)^2) = 2 f(t) \frac{\mathrm{d}f}{\mathrm{d}t}(t)$

resulta

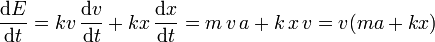
$\frac{\mathrm{d}E}{\mathrm{d}t} = k v\,\frac{\mathrm{d}v}{\mathrm{d}t} + kx\,\frac{\mathrm{d}x}{\mathrm{d}t}=m\,v\,a+k\,x\,v = v(ma+kx)$

pero lo que define al oscilador armónico es que

$ma = - kx\,$

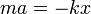
así que, sustituyendo

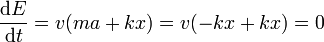
$\frac{\mathrm{d}E}{\mathrm{d}t}=v(ma+kx) = v(-kx+kx) = 0$

y, puesto que la derivada de la energía respecto al tiempo se anula en todo instante, la energía es constante.

2.4.2 A partir de la amplitud y el desfase

El método anterior permite demostrar la constancia de la energía sin necesidad de conocer la solución de la ecuación de movimiento. No obstante, si esta se conoce, el cálculo puede ser más sencillo.

Demostramos antes que una solución general es de la forma

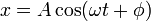
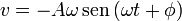$x = A\cos(\omega t+\phi)\,$ $v = -A\omega\,\mathrm{sen}\,(\omega t+\phi)$ \omega=\sqrt{\frac{k}{m}}

Sustituyendo en la expresión de la energía

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): E = \frac{1}{2}mv^2+ \frac{1}{2}kx^2 = \frac{1}{2}mA^2\omega^2\mathrm{sen}^2(\omega t+\phi)+\frac{1}{2}kA^2\cos^2(\omega t+\phi}=\ {}

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \frac{1}{2}kA^2\left(\mathrm{sen}^2(\omega t+\phi)+\cos^2(\omega t+\phi)\right) = \frac{1}{2}kA^2}

2.5 Fórmula de Euler

@@ Línea 108: / Línea 108: @@
 ===Conservación de la energía===
+Existen varias formas de demostrar la conservación de la energía mecánica
+<center><math>E = \frac{1}{2}mv^2+\frac{1}{2}kx^2</math></center>
+====Derivada temporal====
+La forma más general de demostrar que una cantidad es una ''constante de movimiento'' (o ''integral primera'') es probando que su derivada respecto al tiempo se anula.
+En nuestro caso, <math>m</math> y <math>k</math> son constantes del problema, pero <math>x</math> y <math>v</math> son funciones del tiempo, así que la derivada de la energía, aplicando dos veces que
+<center><math>
+\frac{\mathrm{d}\ }{\mathrm{d}t}(f(t)^2) = 2 f(t) \frac{\mathrm{d}f}{\mathrm{d}t}(t)</math></center>
+resulta
+<center><math>\frac{\mathrm{d}E}{\mathrm{d}t} = k v\,\frac{\mathrm{d}v}{\mathrm{d}t} + kx\,\frac{\mathrm{d}x}{\mathrm{d}t}=m\,v\,a+k\,x\,v = v(ma+kx)</math></center>
+pero lo que define al oscilador armónico es que
+<center><math>ma = - kx\,</math></center>
+así que, sustituyendo
+<center><math>\frac{\mathrm{d}E}{\mathrm{d}t}=v(ma+kx) = v(-kx+kx) = 0</math></center>
+y, puesto que la derivada de la energía respecto al tiempo se anula en todo instante, la energía es constante.
+====A partir de la amplitud y el desfase====
+El método anterior permite demostrar la constancia de la energía sin necesidad de conocer la solución de la ecuación de movimiento. No obstante, si esta se conoce, el cálculo puede ser más sencillo.
+Demostramos antes que una solución general es de la forma
+<center><math>x = A\cos(\omega t+\phi)\,</math>{{qquad}}{{qquad}}<math>v = -A\omega\,\mathrm{sen}\,(\omega t+\phi)</math>{{qquad}}{{qquad}}\omega=\sqrt{\frac{k}{m}}</center>
+Sustituyendo en la expresión de la energía
+<center><math>E = \frac{1}{2}mv^2+ \frac{1}{2}kx^2 = \frac{1}{2}mA^2\omega^2\mathrm{sen}^2(\omega t+\phi)+\frac{1}{2}kA^2\cos^2(\omega t+\phi}=\ {}</math><math>\frac{1}{2}kA^2\left(\mathrm{sen}^2(\omega t+\phi)+\cos^2(\omega t+\phi)\right) = \frac{1}{2}kA^2}</math></center>
 ===Fórmula de Euler===
 [[Categoría:Problemas de movimiento oscilatorio]]

Solución general del MAS

De Laplace

Revisión de 12:32 7 feb 2009

Contenido

1 Enunciado

2 Solución

2.1 Valor de a y b

2.2 Velocidad

2.3 Amplitud y desfase

2.4 Conservación de la energía

2.4.1 Derivada temporal

2.4.2 A partir de la amplitud y el desfase

2.5 Fórmula de Euler

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES