Velocidad decreciente con la posición
De Laplace
(→Tiempo de viaje) |
(→Valores particulares de la aceleración) |
||
| Línea 91: | Línea 91: | ||
| -0.75 | | -0.75 | ||
| -0.50 | | -0.50 | ||
| - | | -0. | + | | -0.25 |
|} | |} | ||
última version al 17:17 18 feb 2006
Contenido |
1 Enunciado
Mediante una serie de sensores se mide la velocidad de un vehículo en puntos equiespaciados, obteniéndose la tabla
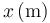
| 0.0 | 100.0 | 200.0 | 300.0 | 400.0 | 500.0 |
|---|---|---|---|---|---|---|
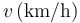
| 108 | 90 | 72 | 54 | 36 | 18 |
- ¿Qué ley sencilla cumple la velocidad como función de la posición?
- Determine la aceleración como función de x. ¿Se trata de un movimiento uniformemente acelerado?
- Halle el valor de la aceleración en cada uno de los puntos de medida.
- Calcule el tiempo empleado en recorrer los 500 m. Si continúa con este movimiento, ¿cuánto tardará en recorrer 600 m?
2 Velocidad como función de la posición
Antes de nada, pasamos los valores de las velocidades al SI. Para pasar km/h a m/s hay que multiplicar por el factor de conversión
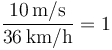
Esto nos da la tabla
|
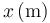
| 0.0 | 100.0 | 200.0 | 300.0 | 400.0 | 500.0 |
|---|---|---|---|---|---|---|
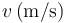
| 30 | 25 | 20 | 15 | 10 | 5 |
y de aquí es inmediato ver qué ley cumple la velocidad como función de la posición:
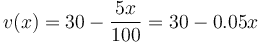
estando la posición medida en metros y la velocidad en m/s.
3 Aceleración como función de la posición
La aceleración se obtiene derivando la velocidad respecto al tiempo. Puesto que lo que tenemos es la velocidad como función de la posición, para hallar la aceleración debemos emplear la regla de la cadena
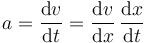
La derivada de la posición respecto al tiempo es justamente la velocidad, por lo que
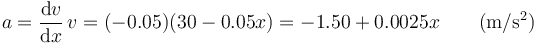
donde la aceleración se mide en m y la aceleración en m/s².
Puesto que la aceleración va variando con la posición, no se trata de un movimiento uniformemente acelerado.
4 Valores particulares de la aceleración
Para hallar la aceleración en posiciones concretas basta con sustituir en la fórmula anterior o aplicar que en este caso
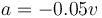
Esto nos da la tabla
|
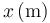
| 0.0 | 100.0 | 200.0 | 300.0 | 400.0 | 500.0 |
|---|---|---|---|---|---|---|
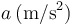
| -1.50 | -1.25 | -1.00 | -0.75 | -0.50 | -0.25 |
Vemos que, como la velocidad, va disminuyendo linealmente con la posición.
5 Tiempo de viaje
Para obtener la posición como función del tiempo debemos integrar la ecuación
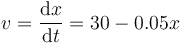
Sin embargo, esto no puede hacerse integrando alegremente respecto al tiempo (¡ni mucho menos respecto a la posición!), ya que en el segundo miembro aparece la propia posición que queremos hallar.
Esto se resuelve escribiendo la ecuación en la forma
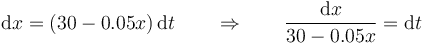
que nos da el tiempo dt necesario para recorrer una pequeña distancia dx. Sumando todos los diferenciales (esto es, integrando), obtenemos el tiempo necesario en llegar a cualquier posición.
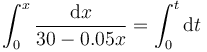
Calculando las dos integrales
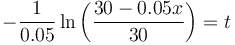
Para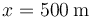 
se requiere un tiempo
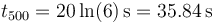
Parecería que, si en vez de recorrer 500 m pedimos que recorra 600, tardará como un 20% más. Pero no es así. Sustituyendo x por 600 nos queda
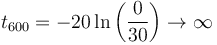
es decir, requiere un tiempo infinito para recorrer esta distancia. La razón es que la velocidad está decayendo exponencialmente con el tiempo, por lo que cada nuevo avance requiere cada vez más tiempo.
