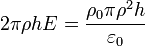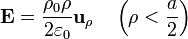Campo de una distribución cilíndrica

De Laplace

(Diferencias entre revisiones)

Revisión de 13:55 16 ene 2009

Contenido

1 Enunciado
2 Solución

1 Enunciado

Un cilindro de radio

a

y longitud indefinida, mucho mayor que el radio, está relleno de sendas distribuciones de carga eléctrica de signo opuesto y densidades volumétricas constantes

ρ 0

y

- ρ 0

, según se muestra en la figura. Además, en la superficie de separación entre ambas distribuciones,

ρ = a / 2

, existe una distribución superficial uniforme de carga.

Calcule el valor de dicha densidad superficial de carga si el campo eléctrico es nulo en los puntos exteriores al cilindro
Obtenga la expresión del campo eléctrico en todo el espacio
Calcule la diferencia de potencial entre el centro de la distribución y la superficie exterior.
Halle la densidad de energía electrostática en cualquier punto del espacio, así como la energía almacenada entre dos planos $z = 0$ y $z = h$ .

2 Solución

2.1 Densidad superficial de carga

Si el campo exterior es nulo, al calcular su flujo a través de una superficie cilíndrica de radio $ρ$ y altura $h$ , exterior al cilindro de carga el flujo es nulo. Esto quiere decir, por aplicación de la ley de Gauss, que también lo es la carga encerrada en este cilindro

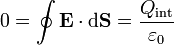
$0 = \oint\mathbf{E}\cdot\mathrm{d}\mathbf{S}= \frac{Q_\mathrm{int}}{\varepsilon_0}$

A su vez la carga encerrada es la suma de la carga de volumen y de la superficial

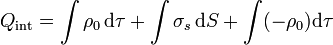
$Q_\mathrm{int}=\int\rho_0\,\mathrm{d}\tau+\int \sigma_s\,\mathrm{d}S+\int(-\rho_0)\mathrm{d}\tau$

Como las tres distribuciones son uniformes, la contribución de cada una es igual al integrando multiplicado por el dominio de integración (un cilindro, una superficie cilíndrica y una corona cilíndrica), esto es

Cilindro interior

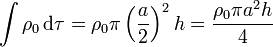
$\int \rho_0\,\mathrm{d}\tau = \rho_0 \pi \left(\frac{a}{2}\right)^2 h=\frac{\rho_0\pi a^2h}{4}$

Superficie cilíndrica intermedia

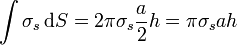
$\int\sigma_s\,\mathrm{d}S = 2\pi\sigma_s\frac{a}{2}h=\pi\sigma_s a h$

Corona cilíndrica exterior

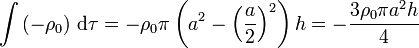
$\int \left(-\rho_0\right)\,\mathrm{d}\tau = -\rho_0 \pi \left(a^2-\left(\frac{a}{2}\right)^2\right) h = -\frac{3\rho_0\pi a^2h}{4}$

Sumando las tres contribuciones e imponiendo la anulación

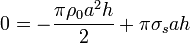
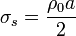
$0 = -\frac{\pi \rho_0a^2 h}{2}+\pi\sigma_sa h$ $\Rightarrow$ $\sigma_s =\frac{\rho_0a}{2}$

2.2 Campo eléctrico

Una vez que tenemos las densidades de carga podemos hallar el campo eléctrico aplicando la ley de Gauss en forma integral.

Por la simetría del sistema podemos considerar que el potencial eléctrico depende exclusivamente de la distancia al eje del cilindro y por tanto el campo eléctrico es radial y dependiente de esta misma distancia

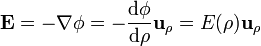
$\phi = \phi(\rho)\,$ $\Rightarrow$ $\mathbf{E}=-\nabla\phi = -\frac{\mathrm{d}\phi}{\mathrm{d}\rho}\mathbf{u}_\rho = E(\rho)\mathbf{u}_\rho$

Si consideramos una superficie cilíndrica de altura $h$ y radio $ρ < a$ , el flujo del campo eléctrico a través de esta superficie contiene solamente la contribución de la cara lateral, en la cual el módulo del campo es constante

$\oint \mathbf{E}\cdot\mathrm{d}\mathbf{S} = \int_{S_L} \left(E(\rho)\mathbf{u}_\rho\right)\cdot\left(\mathrm{d}S\mathbf{u}_\rho\right) = 2\pi\rho h E(\rho)$

Este flujo debe ser igual a la carga encerrada dividida por $\varepsilon_0$ . Tenemos tres posibilidades

2.2.1 En el cilindro interior

Si consideramos $ρ < a / 2$ , la carga encerrada es la contenida en un volumen cilíndrico de radio $ρ$ con densidad uniforme $ρ 0$

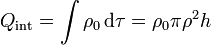
$Q_\mathrm{int}=\int \rho_0\,\mathrm{d}\tau = \rho_0 \pi \rho^2 h$

Aplicando la ley de Gauss

$2\pi\rho h E = \frac{\rho_0\pi \rho^2h}{\varepsilon_0}$ $\Rightarrow$ $\mathbf{E}=\frac{\rho_0\rho}{2\varepsilon_0}\mathbf{u}_\rho\quad \left(\rho<\frac{a}{2}\right)$

2.3 Diferencia de potencial

2.4 Densidad de energía electrostática

@@ Línea 41: / Línea 41: @@
 <center><math>\oint \mathbf{E}\cdot\mathrm{d}\mathbf{S} = \int_{S_L} \left(E(\rho)\mathbf{u}_\rho\right)\cdot\left(\mathrm{d}S\mathbf{u}_\rho\right) = 2\pi\rho h E(\rho)</math></center>
+Este flujo debe ser igual a la carga encerrada dividida por <math>\varepsilon_0</math>. Tenemos tres posibilidades
+====En el cilindro interior====
+Si consideramos <math>\rho < a/2</math>, la carga encerrada es la contenida en un volumen cilíndrico de radio <math>\rho</math> con densidad uniforme <math>\rho_0</math>
+<center><math>Q_\mathrm{int}=\int \rho_0\,\mathrm{d}\tau = \rho_0 \pi \rho^2 h</math></center>
+Aplicando la ley de Gauss
+<center><math>2\pi\rho h E = \frac{\rho_0\pi \rho^2h}{\varepsilon_0}</math>{{tose}}<math>\mathbf{E}=\frac{\rho_0\rho}{2\varepsilon_0}\mathbf{u}_\rho\quad \left(\rho<\frac{a}{2}\right)</math></center>
 ===Diferencia de potencial===

Campo de una distribución cilíndrica

De Laplace

Revisión de 13:55 16 ene 2009

Contenido

1 Enunciado

2 Solución

2.1 Densidad superficial de carga

2.2 Campo eléctrico

2.2.1 En el cilindro interior

2.3 Diferencia de potencial

2.4 Densidad de energía electrostática

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES