Propiedades del agua
De Laplace
(→Diagrama V-T y p-V) |
(→Diagrama V-T y p-V) |
||
| Línea 195: | Línea 195: | ||
En este tramo tenemos la mezcla saturada. Pasamos de 100% de agua líquida (y 0% de vapor) en el extremo izquierdo a 100% de vapor de agua en el extremo derecho. Para un punto intermedio habrá una cierta proporción de cada fase. Se denomina ''calidad'' (o ''título'') del vapor a la fracción molar del vapor de agua en la mezcla. Así un vapor con un título del 80% quiere decir que el 80% de los moles son de vapor de agua y el 20% de agua líquida. Dado que el vapor y el agua tienen el mismo peso molecular, la calidad también equivale a la fracción de masa de vapor. En general, la calidad puede calcularse observando que las propiedades extensivas, como el volumen varían linealmente con la fracción molar | En este tramo tenemos la mezcla saturada. Pasamos de 100% de agua líquida (y 0% de vapor) en el extremo izquierdo a 100% de vapor de agua en el extremo derecho. Para un punto intermedio habrá una cierta proporción de cada fase. Se denomina ''calidad'' (o ''título'') del vapor a la fracción molar del vapor de agua en la mezcla. Así un vapor con un título del 80% quiere decir que el 80% de los moles son de vapor de agua y el 20% de agua líquida. Dado que el vapor y el agua tienen el mismo peso molecular, la calidad también equivale a la fracción de masa de vapor. En general, la calidad puede calcularse observando que las propiedades extensivas, como el volumen varían linealmente con la fracción molar | ||
| - | <center><math> V=x_L V_L + x_v V_v = V_L + x_v( | + | <center><math> V=x_L V_L + x_v V_v = (1+x_v) V_L + x_v V_v= V_L + x_v(V_v-V_L)\qquad \Rightarrow\qquad x_v=\frac{V-V_L}{V_v-V_L}</math></center> |
siendo <math>V_L</math> el volumen ocupado si hay un 100% de agua y <math>V_v</math> su valor si hay un 100% de vapor. | siendo <math>V_L</math> el volumen ocupado si hay un 100% de agua y <math>V_v</math> su valor si hay un 100% de vapor. | ||
Revisión de 10:18 27 feb 2016
Contenido |
1 Introducción
La importancia del agua en la ingeniería difícilmente puede ser exagerada, ya que aparece en toda clase de aplicaciones. En el campo de la termodinámica técnica, es el componente esencial de las máquinas de vapor, entre otras aplicaciones.
A modo de introducción, en este artículo se comentan algunas de las propiedades de esta sustancia. En especial, sus aspectos termodinámicos de su fase líquida, de su fase gaseosa y del estado de equilibrio entre ambas.
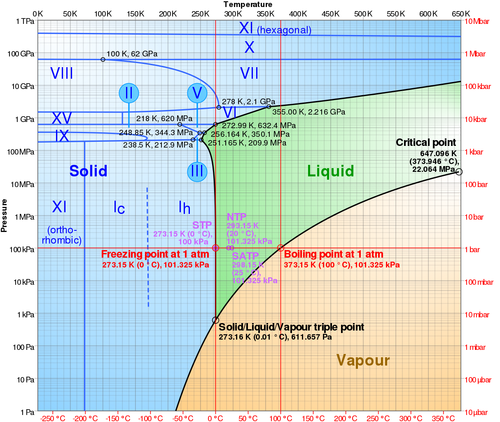
2 Fases del agua
En sus estados más habituales, el agua se presenta en tres formas: una sólida (hielo), una líquida (llamada simplemente agua) y una gaseosa (vapor de agua). No son los únicos estados posibles, ya que existen diferentes formas de hielo, según como cristalice.
A una presión ambiente de 101 kPa (1 atm), el agua se encuentra en forma de hielo por debajo de la temperatura de fusión 273.15 K (0.00°C) y de agua por encima de esta temperatura hasta la temperatura de ebullición 373.13K (99.98°C). Por encima de esta temperatura se encuentra en forma de vapor de agua.
La temperatura de fusión y la de ebullición son funciones de la presión.
- A una presión mayor la temperatura de ebullición se eleva. Así, a una presión de 400 kPa, la temperatura de ebullición es de 417 K (144°C). Este es el principio de las ollas a presión, que consiguen alcanzar una mayor temperatura en forma líquida.
- La temperatura de fusión depende mucho menos de la presión. El agua es excepcional respecto a la mayoría de las sustancias en cuanto a que al aumentar la presión la temperatura de fusión disminuye (normalmente aumenta). Este es el principio que permite patinar sobre hielo. El hielo no es para nada resbaladizo. Sin embargo, al ejercerse una presión sobre él se forma una fina capa de agua que permite el deslizamiento.
Una mezcla de agua y hielo a la temperatura de fusión se encuentra en equilibrio térmico. Ni el hielo se derrite, ni el agua se congela. Asimismo, a la temperatura de ebullición, el agua se encuentra en equilibrio térmico con el vapor de agua.
Existe una presión a la cual la temperatura de fusión y la de ebullición se igualan. A la presión de 611.73 Pa (6.11 mbar) y la temperatura de 273.16 K se produce el equilibrio térmico entre las tres fases. A este punto se lo conoce como punto triple del agua.
3 Propiedades del agua
Si tenemos una cantidad de agua (líquida) a una cierta temperatura y la presión a la que se encuentra es superior a la que produciría ebullición a esa temperatura, se dice que es un líquido comprimido (ya que la presión exterior la mantiene en estado líquido) o líquido subenfriado (ya que se encuentra por debajo de su temperatura de ebullición).
Esta es la situación habitual entre 0°C y 100°C a la presión de una atmósfera. A esta presión, el agua tiene una densidad que es aproximadamente igual a 1000 kg/m³. Esta densidad, no obstante, depende ligeramente de la temperatura
| T(°C) | ρ (kg/m³) | T(°C) | ρ (kg/m³) | T(°C) | ρ (kg/m³) |
|---|---|---|---|---|---|
| 0.01 | 999.8 | 35 | 994.1 | 70 | 978 |
| 5 | 1000 | 40 | 992.3 | 75 | 975 |
| 10 | 999.7026 | 45 | 990.2 | 80 | 972 |
| 15 | 999.1026 | 50 | 988 | 85 | 968 |
| 20 | 998.2071 | 55 | 986 | 90 | 965 |
| 25 | 997.0479 | 60 | 983 | 95 | 962 |
| 30 | 995.6502 | 65 | 980 | 100 | 958 |
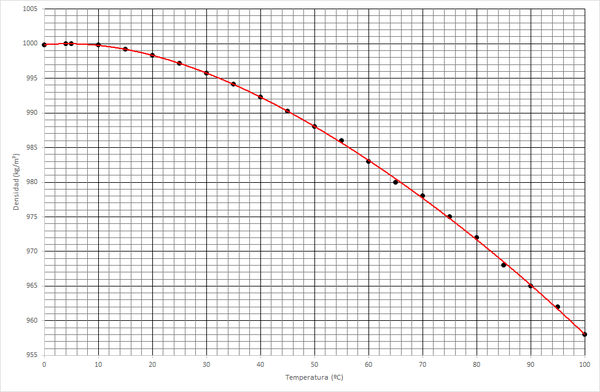
De esta tabla y esta gráfica, salta a la vista otra propiedad del agua que la hace diferente al resto de sustancias: la densidad no disminuye monótonamente, sino que tiene un máximo. Esto quiere decir que, en general el agua caliente es más ligera que el agua fría y por tanto, tenderá a ir hacia la superficie, pero a temperaturas próximas a 0°C la tendencia se invierte y el agua más caliente es más pesada que la fría. El máximo de densidad se alcanza a 4ºC. Esto es lo que se conoce como anomalía térmica del agua.
Esta propiedad permite que el agua de un lago no se congele por completo. Si no hubiera anomalía, el agua más caliente quedaría en la superficie, donde se iría enfriando, cayendo al fondo y siendo sustituida por agua caliente, que se enfriaría a su vez, etc, hasta que todo quedara congelado. Al existir la anomalía esto no se produce porque el agua más caliente se queda abajo y el calor solo se pierde por conducción y no por convección, lo que es mucho más lento.
A partir de estos valores puede hallarse el coeficiente de dilatación volumétrica
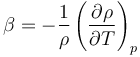
que a 4°C se anula y a 20°C vale
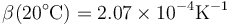
El agua es un líquido que se puede tratar como incompresible, ya que su coeficiente de compresibilidad es extremadamente pequeño. A 20°C y 100 kPa
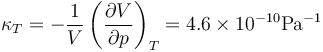
o, equivalentemente, su módulo de compresibilidad es
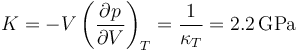
Esto quiere decir que para rangos ordinarios de presiones puede suponerse que el volumen (o la densidad) dependen exclusivamente de la temperatura, pero que incluso esta dependencia es pequeña.
El agua posee un calor específico que también es función de la temperatura pero que, de nuevo, varía poco en el el rango de 0°C a 100°C, siendo su valor
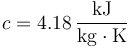
4 Propiedades del vapor de agua
Por encima de la temperatura de ebullición, el agua se encuentra en forma gaseosa. Al ser la temperatura superior a Tb, se dice que el vapor está sobrecalentado.
El vapor de agua no siempre se puede tratar como un gas ideal, ya que la cohesión entre sus moléculas provoca que se aleje de la hipótesis de gas ideal (que supone que las partículas no interactúan entre sí). No obstante, para altas temperaturas y bajas presiones (comparadas con las de saturación) se puede hacer esta aproximación, al menos como primera estimación de los resultados.
5 Equilibrio agua-vapor
Cuando consideramos posibles situaciones con agua y vapor de agua (no consideramos el hielo) tenemos tres posibilidades: que tengamos solo agua, que tengamos un equilibrio de agua y vapor, o que tengamos solo vapor.
El criterio que nos permite establecer cuál de las tres situaciones se va a dar lo da la curva de saturación. Esta curva da la temperatura de ebullición como función de la presión (o viceversa):
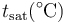
| psat(kPa) |
|---|---|
| 0 | 0.6105 |
| 5 | 0.8722 |
| 10 | 1.228 |
| 20 | 2.338 |
| 30 | 4.243 |
| 40 | 7.376 |
| 50 | 12.33 |
| 60 | 19.92 |
| 70 | 31.16 |
| 80 | 47.34 |
| 90 | 70.10 |
| 100 | 101.3 |
Esta una tabla experimental a la cual se puede ajustar con bastante aproximación una curva casi exponencial
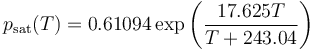(p en kPa, T en °C)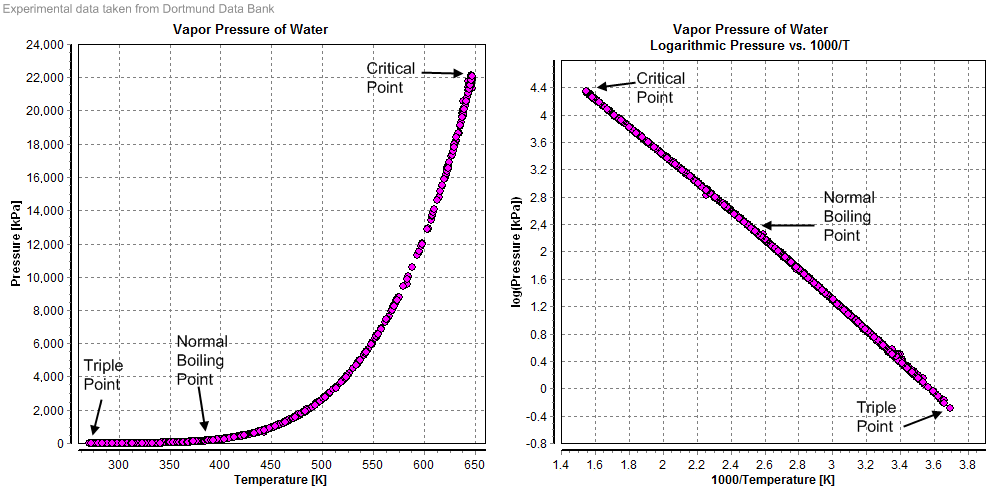
Para una presión dada, si la temperatura es menor a la de saturación tenemos solo agua en la fase líquida (luego veremos que no es exactamente así). Se dice que tenemos agua subenfriada. Si la temperatura es superior a la de saturación tenemos vapor sobrecalentado. A la temperatura de saturación se produce equilibrio de fases y térmico entre las dos fases, que se dicen saturadas (o que tenemos una mezcla saturada).
Para entender el papel de la curva de saturación consideraremos tres situaciones: Un recipiente hermético rígido solo con agua; un recipiente solo con agua cerrado por un pistón; y un recipiente abierto al aire.
- Si tenemos un recipiente rígido en el que se ha hecho el vacío absoluto y posteriormente se introduce agua sin llenarlo por completo, se produce rápidamente la formación de vapor, ya que algunas moléculas tienen energía suficiente para abandonar la fase líquida. Este proceso se detiene cuando se alcanza la saturación. Cuando la presión y la temperatura son las de saturación se produce el equilibrio de fases. Cualquier nueva molécula que escapa del agua es compensada por una que vuelve a ella.
- Si tenemos el mismo recipiente pero ahora en vez de ser rígido está cerrado por un émbolo y desde fuera aplicamos una presión exterior pext (la atmosférica, por ejemplo), superior a la de saturación a la temperatura del sistema, la presión del vapor que se forma no es capaz de soportar el émbolo, empujado desde fuera, por lo que este impide la formación del vapor y tenemos solo agua subenfriada. Si se formara una burbuja en el líquido lo haría a la presión de saturación a esa temperatura. Puesto que la presión exterior es superior, la burbuja no puede llegar a formarse.
- Si ahora en este mismo recipiente vamos subiendo la temperatura hasta que la presión de saturación correspondiente iguale a la presión exterior, entonces el vapor es ya capaz de compensar la presión exterior y permanecer en forma gaseosa. Es más, cualquier burbuja que se forme en el interior del líquido lo hace también a esa presión, por lo que no desaparece, sino que por el principio de Arquímedes se ve empujada hacia arriba. El agua pasa a la forma gaseosa de forma turbulenta, burbujeando. Se dice que ha entrado en ebullición. Por eso la temperatura de ebullición es la misma que la de saturación.
- En el caso de un recipiente abierto al aire tenemos dos posibilidades: que el agua esté en equilibrio o que no lo esté. Si está en equilibrio, se debe a que en el aire existe una cierta cantidad de vapor de agua, de forma que la presión parcial (es decir, la parte de la presión total debida al vapor de agua) iguala a la presión de saturación a esa temperatura. Por ejemplo, a 20 °C, y 101.3 kPa, la presión de saturación (o presión de vapor, como se llama en este contexto) es de 2.3 kPa. Puesto que la total es de 101.3 kPa, la proporción de moléculas de agua debe ser un 2.3% del total de moléculas del aire. Se dice que tenemos aire húmedo saturado, con una humedad relativa del 100%. Con esta humedad relativa, cualquier nueva molécula que escape del agua es compensada con una que vuelve a ella y se mantiene la situación de equilibrio.
- Si el aire que ejerce la presión exterior está seco, o tiene una presión parcial inferior a la de saturación (o, dicho de otra forma, con una humedad relativa inferior al 100%), entonces no hay equilibrio de fases. Las moléculas que escapan del agua no se compensan por otras que vuelven, por lo que el líquido va pasando gradualmente a la fase gaseosa sin ebullición. Se dice que tenemos evaporación. Esta es la razón porque los charcos y la ropa se secan expuestos al aire seco, pero no si hay mucha humedad en el aire. ¿De qué sirve que le de el sol a la ropa? La radiación solar no está en equilibrio térmico, sino que se encuentra a una temperatura muy superior y proporciona más energía a las moléculas para que escapen al aire, acelerando el proceso. Pero de nuevo, si el aire está saturado, tampoco así se secaría la ropa.
6 Diagrama V-T y p-V
Si representamos en una gráfica como varía el volumen de una cierta cantidad de agua al aumentar la temperatura a una presión constante obtenemos tres tramos (no consideramos la presencia del hielo):
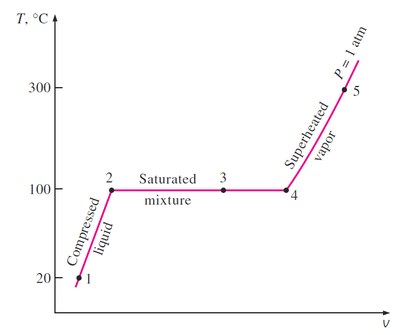
Para temperaturas por debajo de la de saturación, tenemos agua subenfriada y el volumen varía muy ligeramente por efecto de la temperatura. Hay dilatación volumétrica, pero esta es pequeña. Esto se representa por una línea que es casi vertical.
Cuando se alcanza la temperatura de saturación (o de ebullición) el agua comienza a convertirse en vapor. Puesto que el vapor es mucho menos denso que el agua (la densidad del vapor de agua a 1 bar y 100°C es de 0.6kg/m³, mientras que la densidad del agua es 960kg/m³, del orden de 2000 veces la del vapor), el volumen aumenta al producirse el cambio de fase. Durante este proceso no se modifica la temperatura. Varía la cantidad de agua y de vapor, pero siguen en equilibrio térmico. El tramo correspondiente en la gráfica es una línea horizontal.
En este tramo tenemos la mezcla saturada. Pasamos de 100% de agua líquida (y 0% de vapor) en el extremo izquierdo a 100% de vapor de agua en el extremo derecho. Para un punto intermedio habrá una cierta proporción de cada fase. Se denomina calidad (o título) del vapor a la fracción molar del vapor de agua en la mezcla. Así un vapor con un título del 80% quiere decir que el 80% de los moles son de vapor de agua y el 20% de agua líquida. Dado que el vapor y el agua tienen el mismo peso molecular, la calidad también equivale a la fracción de masa de vapor. En general, la calidad puede calcularse observando que las propiedades extensivas, como el volumen varían linealmente con la fracción molar
siendo VL el volumen ocupado si hay un 100% de agua y Vv su valor si hay un 100% de vapor.
El estudio de la calidad de vapor es importante porque en una turbina no interesa que al enfriarse el vapor se formen gotitas de agua que dañan la estructura. Interesa entonces que el vapor esté a una temperatura superior a la de saturación, es decir, esté sobrecalentado.
Llega un momento en que todo el agua se convierte en vapor. A partir de ahí, ya el comportamiento es el de un gas, aunque no ideal. Tenemos vapor sobrecalentado. Para que el vapor de agua pueda tratarse como un gas ideal es necesario que su temperatura sea muy alta o su presión muy baja. No obstante, la ecuación del gas ideal sirve para dar una estimación de los resultados.
Si consideramos la misma gráfica pero para una presión superior obtenemos una nueva isobara por encima de la que teníamos, ya que la temperatura de saturación aumenta con la presión. Vemos que es menor la diferencia entre los volúmenes ocupados por el agua saturada (a punto de entrar en ebullición) y el vapor saturado (cuando justo todo el agua se ha convertido en vapor). Los dos puntos se van acercando hasta que se llega al llamado punto crítico, a partir del cual el agua se convierte en vapor sin que haya un cambio de fase, sino una variación continua.
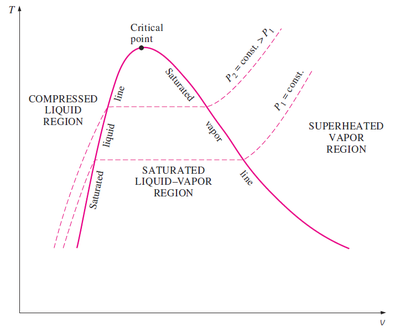
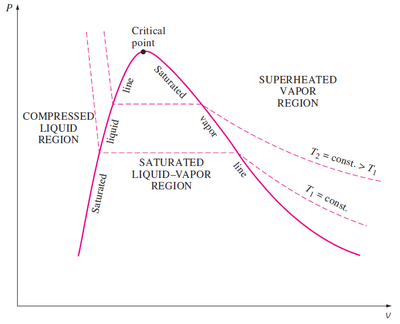
Si trazamos la gráfica de las isotermas, considerando la variación del volumen con la presión obtenemos una curva similar. A la izquierda tenemos el líquido comprimido o subenfriado, en el cual las isotermas son casi verticales, pues el agua es prácticamente incompresible. Luego sigue una recta horizontal,, mientras se produce el cambio de fase a presión constante. Cuando se completa esta y solo tenemos vapor sobrecalentado, el comportamiento es aproximadamente hiperbólico, como diría la ley de Boyle.
La dependencia conjunta entre presión, volumen y temperatura puede representarse como una superficie en tres dimensiones. La tres vistas corresponden a los tres tipos de gráfica: V-T (planta), p-V (alzado) y p-T (perfil). En esta gráfica, el punto triple se ve como una línea triple, ya que para una misma presión y temperatura puede haber diferentes volúmenes, según la proporción de hielo, agua y vapor que tengamos.
