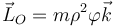Leyes de conservación en polares y cilíndricas
De Laplace
(Página creada con '==Enunciado== Una partícula de masa <math>m</math> describe el movimiento expresado en cilíndricas <center><math>\rho = \sqrt{A+Bt^2}\qquad\qquad \varphi = \mathrm{arctg}\lef…') |
|||
| Línea 12: | Línea 12: | ||
<center><math>\rho = A\qquad\qquad \varphi = \omega t\qquad\qquad z = v_0t</math></center> | <center><math>\rho = A\qquad\qquad \varphi = \omega t\qquad\qquad z = v_0t</math></center> | ||
| + | ==Fórmulas generales== | ||
| + | ===Cantidad de movimiento=== | ||
| + | La cantidad de movimiento de una partícula es el producto de su masa por su velocidad. La expresión de ésta, en coordenadas cilíndricas, es | ||
| + | |||
| + | <center><math>\vec{v}=\dot{\rho}\vec{u}_\rho+\rho\dot{\varphi}\vec{u}_\varphi+\dot{z}\vec{k}</math></center> | ||
| + | |||
| + | por lo que la cantidad de movimiento es | ||
| + | |||
| + | <center><math>\vec{p}=m\dot{\rho}\vec{u}_\rho+m\rho\dot{\varphi}\vec{u}_\varphi+m\dot{z}\vec{k}</math></center> | ||
| + | |||
| + | En el caso particular de movimiento en el plano OXY, la expresión se reduce a la de coordenadas polares | ||
| + | |||
| + | <center><math>\vec{p}=m\dot{\rho}\vec{u}_\rho+m\rho\dot{\varphi}\vec{u}_\varphi</math></center> | ||
| + | |||
| + | ===Momento cinético=== | ||
| + | <math>\vec{L}_O</math> es igual al momento de la cantidad de movimiento, siendo el vector de posición en cilíndricas | ||
| + | |||
| + | <center><math>\vec{r}=\rho\vec{u}_\rho+z\vec{k}</math></center> | ||
| + | |||
| + | por lo que resulta | ||
| + | |||
| + | <center><math>\vec{L}_O=\vec{r}\times\vec{p}=\left|\begin{matrix} \vec{u}_\rho & \vec{u}_\varphi & \vec{k} \\ \rho & 0 & z \\ \dot{\rho} & \rho\dot{\varphi} & \dot{z}\end{matrix}\right|=</math></center> | ||
| + | |||
| + | <center><math>= -mz\rho\dot{\varphi}\vec{u}_\rho+m(z\dot{\rho}-\rho\dot{z})\vec{u}_ºvarphi + \rho^2\dot{\varphi}\vec{k}</math></center> | ||
| + | |||
| + | En el caso de movimiento en el plano OXY el momento se reduce a | ||
| + | |||
| + | <center><math>\vec{L}_O=m\rho^2\varphi\vec{k}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | ==Primer caso== | ||
| + | ==Segundo caso== | ||
[[Categoría:Problemas de energía y leyes de conservación (GIE)]] | [[Categoría:Problemas de energía y leyes de conservación (GIE)]] | ||
Revisión de 10:23 26 nov 2015
Contenido |
1 Enunciado
Una partícula de masa m describe el movimiento expresado en cilíndricas
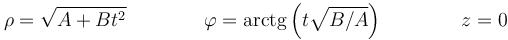
Determine si se conserva la cantidad de movimiento, el momento cinético respecto al origen de coordenadas y la energía cinética. En su caso, halle el valor de las constantes.
Responda a las mismas preguntas para el movimiento helicoidal
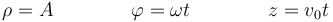
2 Fórmulas generales
2.1 Cantidad de movimiento
La cantidad de movimiento de una partícula es el producto de su masa por su velocidad. La expresión de ésta, en coordenadas cilíndricas, es
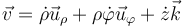
por lo que la cantidad de movimiento es
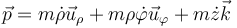
En el caso particular de movimiento en el plano OXY, la expresión se reduce a la de coordenadas polares
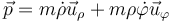
2.2 Momento cinético
es igual al momento de la cantidad de movimiento, siendo el vector de posición en cilíndricas
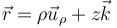
por lo que resulta
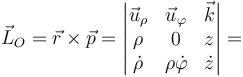
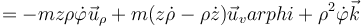
En el caso de movimiento en el plano OXY el momento se reduce a
