Péndulo con dos masas
De Laplace
| Línea 1: | Línea 1: | ||
| + | ==Enunciado== | ||
Para hacer un experimento con un péndulo se toma una varilla muy ligera (que se puede suponer sin masa), de 100cm, con orificios cada 25cm comenzando desde el extremo. En uno de los extremos (1<sup>er</sup> orificio) se atornilla una masa de 2 kg, en el otro extremo (5º orificio) una de 1 kg y la varilla se cuelga de la pared por el 2º orificio. La varilla se sitúa horizontalmente y se suelta partiendo del reposo. | Para hacer un experimento con un péndulo se toma una varilla muy ligera (que se puede suponer sin masa), de 100cm, con orificios cada 25cm comenzando desde el extremo. En uno de los extremos (1<sup>er</sup> orificio) se atornilla una masa de 2 kg, en el otro extremo (5º orificio) una de 1 kg y la varilla se cuelga de la pared por el 2º orificio. La varilla se sitúa horizontalmente y se suelta partiendo del reposo. | ||
| Línea 12: | Línea 13: | ||
Tómese <math>g = 10\,\mathrm{m}/\mathrm{s}^2</math>. | Tómese <math>g = 10\,\mathrm{m}/\mathrm{s}^2</math>. | ||
| + | ==Velocidades== | ||
| + | En este sistema se conserva la energía mecánica, por lo que podemos igualar su valor en la posición horizontal con el que tiene en la vertical. | ||
| + | |||
| + | ===Posición horizontal=== | ||
| + | La energía cinética es 0, porque parte del reposo, y para la potencial, podemos medir la altura desde esta posición, por lo que también se anula | ||
| + | |||
| + | <center><math>E_i =K_i + U_i = 0\,</math></center> | ||
| + | |||
| + | ===Posición vertical=== | ||
| + | Impulsada por la gravedad, la barra oscila y llega a ponerse vertical. ¿Cuál de las dos masas ocupa la posición inferior? La que haga disminuir la energía potencial (el sistema tiende a la posición de mínima energía). Esto se consigue si la masa que baja es la de 1kg (que baja 75cm) y la que sube es la de 2kg (que sube 25cm). La energía potencial final es | ||
| + | |||
| + | <center><math>U_f = m_1 g b_1+m_2 g (-b_2) =\left(2\times 10 \times 0.25-1\times 10\times 0.75\right)\,\mathrm{J}=-2.5\,\mathrm{J}</math></center> | ||
| + | |||
| + | Para la energía cinética, observamos que cada masa describe un movimiento circular alrededor del punto de anclaje, por lo que | ||
| + | |||
| + | <center><math>K_f = \frac{1}{2}m_1(\omega b_1)^2 +\frac{1}{2}m_2(\omega b_2)^2 = \frac{m_1b_1^2+m_2b_2^2}{2}\omega^2= 0.34375\omega^2</math></center> | ||
| + | |||
| + | ===Conservación de la energía=== | ||
| + | Aplicamos la ley de conservación de la energía mecánica y queda | ||
| + | |||
| + | <center><math>0 = \frac{m_1b_1^2+m_2b_2^2}{2}\omega^2+(m_1b_1-m_2b_2)g </math></center> | ||
| + | |||
| + | de donde | ||
| + | |||
| + | <center><math>\omega=\sqrt{\frac{2(m_2b_2-m_1b_1)g}{m_1b_1^2+m_2b_2^2}}</math></center> | ||
| + | |||
| + | con el valor numérico | ||
| + | |||
| + | <center><math>\omega = \sqrt{\frac{2.5}{0.34375}}\,\frac{\mathrm{rad}}{\mathrm{s}}=2.70\,\frac{\mathrm{rad}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | Si hubiéramos supuesto que la que baja es la otra pesa, nos hubiera salido que la energía potencial aumenta y queda una velocidad angular imaginaria, lo que es imposible. | ||
| + | |||
| + | La velocidad lineal de la pesa 1 es | ||
| + | |||
| + | <center><math>\vec{v}_1=\omega b_1\vec{\imath}=0.674\vec{\imath}\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | y la de la pesa 2 | ||
| + | |||
| + | <center><math>\vec{v}_2=-\omega b_1\vec{\imath}=-2.03\vec{\imath}\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | ==Cantidad de movimiento y momento cinético== | ||
| + | ==Tensiones== | ||
| + | ==Fuerza en el anclaje== | ||
[[Categoría:Problemas de energía y leyes de conservación (GIE)]] | [[Categoría:Problemas de energía y leyes de conservación (GIE)]] | ||
Revisión de 17:24 2 sep 2015
Contenido[ocultar] |
1 Enunciado
Para hacer un experimento con un péndulo se toma una varilla muy ligera (que se puede suponer sin masa), de 100cm, con orificios cada 25cm comenzando desde el extremo. En uno de los extremos (1er orificio) se atornilla una masa de 2 kg, en el otro extremo (5º orificio) una de 1 kg y la varilla se cuelga de la pared por el 2º orificio. La varilla se sitúa horizontalmente y se suelta partiendo del reposo.

Para el instante en que pasa por primera vez por la posición vertical, calcule:
- La velocidad angular de la barra y la velocidad lineal de cada masa.
- La cantidad de movimiento del sistema y el momento cinético respecto al punto de anclaje O.
- La tensión de la varilla en el tramo entre cada masa y el punto de anclaje.
- La fuerza sobre el punto de anclaje.
Tómese 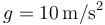 .
.
2 Velocidades
En este sistema se conserva la energía mecánica, por lo que podemos igualar su valor en la posición horizontal con el que tiene en la vertical.
2.1 Posición horizontal
La energía cinética es 0, porque parte del reposo, y para la potencial, podemos medir la altura desde esta posición, por lo que también se anula

2.2 Posición vertical
Impulsada por la gravedad, la barra oscila y llega a ponerse vertical. ¿Cuál de las dos masas ocupa la posición inferior? La que haga disminuir la energía potencial (el sistema tiende a la posición de mínima energía). Esto se consigue si la masa que baja es la de 1kg (que baja 75cm) y la que sube es la de 2kg (que sube 25cm). La energía potencial final es

Para la energía cinética, observamos que cada masa describe un movimiento circular alrededor del punto de anclaje, por lo que
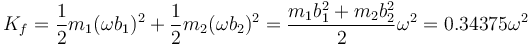
2.3 Conservación de la energía
Aplicamos la ley de conservación de la energía mecánica y queda

de donde
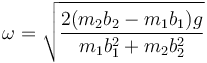
con el valor numérico

Si hubiéramos supuesto que la que baja es la otra pesa, nos hubiera salido que la energía potencial aumenta y queda una velocidad angular imaginaria, lo que es imposible.
La velocidad lineal de la pesa 1 es
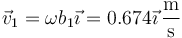
y la de la pesa 2