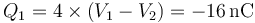Dos esferas conductoras concéntricas
De Laplace
(→Potenciales en función de las cargas) |
(→Potenciales en función de las cargas) |
||
| Línea 54: | Línea 54: | ||
<center><math>Q_a = Q_1\qquad\qquad Q_b = -Q_1\qquad\qquad Q_c = Q_2-Q_b = Q_2+Q_1</math></center> | <center><math>Q_a = Q_1\qquad\qquad Q_b = -Q_1\qquad\qquad Q_c = Q_2-Q_b = Q_2+Q_1</math></center> | ||
===Potenciales en función de las cargas=== | ===Potenciales en función de las cargas=== | ||
| - | Aplicando el resultado anterior tenemos, para el potencial de la esfera maciza | + | Aplicando el resultado anterior tenemos, |
| + | |||
| + | ====Superficie de radio ''a''==== | ||
| + | Para el potencial de la esfera maciza, tenemos una superficie que es coincidente de la de radio <math>a</math>, está en el interior de la de radio <math>b</math> y en el interior de la de radio <math>c</math>. Para las dos últimas el potencial es el correspondiente al interior de una superficie cargada y para la primera es indiferente que usemos el interior o el exterior, ya que ambos coinciden sobre la propia superficie. | ||
| + | |||
| + | El potencial de la superficie de radio <math>a</math> coincide con el potencial de toda la esfera maciza, que es el conductor 1. | ||
<center><math>V_1 = V_a=\frac{Q_a}{4\pi\varepsilon_0a}+\frac{Q_b}{4\pi\varepsilon_0 b}+\frac{Q_c}{4\pi\varepsilon_0c}</math></center> | <center><math>V_1 = V_a=\frac{Q_a}{4\pi\varepsilon_0a}+\frac{Q_b}{4\pi\varepsilon_0 b}+\frac{Q_c}{4\pi\varepsilon_0c}</math></center> | ||
| Línea 60: | Línea 65: | ||
Sustituyendo las cargas en cada superficie | Sustituyendo las cargas en cada superficie | ||
| - | <center><math>V_1 = \frac{Q_1}{4\pi\varepsilon_0a}+\frac{-Q_1}{4\pi\varepsilon_0 b}+\frac{Q_1+Q_2}{4\pi\varepsilon_0c}=\left(\frac{1}{4\pi\varepsilon_0a}-\frac{1}{4\pi\varepsilon_0b}+\frac{1}{4\pi\varepsilon_0c}\right)Q_1+\left(\frac{1}{4\pi\varepsilon_0c}\right)Q_2</math></center> | + | <center><math>V_1 = V_a= \frac{Q_1}{4\pi\varepsilon_0a}+\frac{-Q_1}{4\pi\varepsilon_0 b}+\frac{Q_1+Q_2}{4\pi\varepsilon_0c}=\left(\frac{1}{4\pi\varepsilon_0a}-\frac{1}{4\pi\varepsilon_0b}+\frac{1}{4\pi\varepsilon_0c}\right)Q_1+\left(\frac{1}{4\pi\varepsilon_0c}\right)Q_2</math></center> |
| - | Para la pared del hueco | + | ====Superficie de radio b==== |
| + | Para la pared del hueco, tenemos una superficie que está fuera de la de radio <math>a</math>, coincidente con la de radio <math>b</math> y dentro de la de radio <math>c</math>. Aplicando el potencial correspondiente a cada caso queda | ||
| - | <center><math>V_b = \frac{Q_a}{4\pi\ | + | <center><math>V_b = \frac{Q_a}{4\pi\varepsilon_0\underbrace{b}_{r=b}}+\frac{Q_b}{4\pi\varepsilon_0 b}+\frac{Q_c}{4\pi\varepsilon_c}</math></center> |
que da | que da | ||
| Línea 70: | Línea 76: | ||
<center><math>V_b = \left(\frac{1}{4\pi\varepsilon_0c}\right)Q_1+\left(\frac{1}{4\pi\varepsilon_0c}\right)Q_2</math></center> | <center><math>V_b = \left(\frac{1}{4\pi\varepsilon_0c}\right)Q_1+\left(\frac{1}{4\pi\varepsilon_0c}\right)Q_2</math></center> | ||
| - | Si consideramos la pared exterior de la corona esférica | + | ====Superficie de radio c==== |
| + | Si consideramos la pared exterior de la corona esférica, tenemos ahora una que está fuera de la de radio <math>a</math>, fuera de la de radio <math>b</math> y coincidente con la de radio <math>c</math>, por lo que podemos aplicar el potencial exterior en cada caso | ||
| - | <center><math>V_c = \frac{Q_a}{4\pi\ | + | <center><math>V_c = \frac{Q_a}{4\pi\varepsilon_0\underbrace{c}_{r=c}}+\frac{Q_b}{4\pi\varepsilon_0 \underbrace{c}_{r=c}}+\frac{Q_c}{4\pi\varepsilon_0\underbrace{c}_{r=c}}</math></center> |
que da, de nuevo, | que da, de nuevo, | ||
| Línea 79: | Línea 86: | ||
Este potencial es el mismo que el de la cara interior ya que ambas superficies pertenecen al mismo conductor. Es consecuencia del teorema de Faraday. | Este potencial es el mismo que el de la cara interior ya que ambas superficies pertenecen al mismo conductor. Es consecuencia del teorema de Faraday. | ||
| + | |||
| + | <center><math>V_2 = V_b=V_c\,</math></center> | ||
Numéricamente, en el SI, | Numéricamente, en el SI, | ||
Revisión de 08:57 14 jun 2015
Contenido |
1 Enunciado
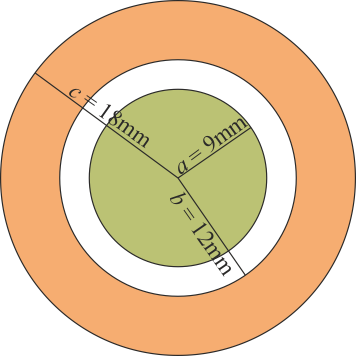
Se construye un sistema de dos conductores metálicos. El “1” es una esfera maciza de radio 9 mm. El “2” es una corona esférica gruesa, concéntrica con la anterior, de radio interior 12 mm y exterior 18 mm. Halle la carga almacenada y el potencial al que se encuentra cada conductor, así como la energía almacenada en el sistema, para los siguientes casos:
- La esfera almacena una carga de +4 nC y la corona está aislada y descargada.
- La esfera está aislada y descargada y la corona almacena +6 nC
- La esfera almacena una carga de +4 nC y la corona de +6 nC
- La esfera almacena una carga de −4 nC y la corona de +4 nC
- La esfera almacena una carga de −4 nC y la corona de +6 nC
- La esfera almacena una carga de +4 nC y la corona está a tierra
- La esfera está a tierra y la corona almacena una carga de +6 nC
- La esfera está a +2 kV y la corona está a tierra.
- La esfera está a tierra y la corona a +2 kV.
- La esfera y la corona están a +2 kV
- La esfera está a +2 kV y la corona está a −2 kV.
Sugerencia: Resuélvase primero el caso general, estableciendo relaciones entre las cargas y los potenciales, y expresiones para la energía. Puede ser útil construir un circuito equivalente.
2 Introducción
Aunque este problema consta de muchos apartados, es fácil ver que todos son muy parecidos, sólo cambia el dato que se da y el valor de cada uno.
Éste es un caso particular de problema del potencial. Tenemos un sistema de conductores (dos, en este caso), que se encuentran en equilibrio electrostático. De cada conductor, sabemos que su potencial es el mismo en todos sus puntos, pero no necesariamente cuanto vale éste.
Para cada conductor hay que dar o bien su voltaje o bien su carga total (pero no como está distribuida ésta), nunca las dos cosas a la vez. Eso sería redundante o contradictorio. A partir de esta información se puede determinar las cargas o potenciales que se desconocen, resolviendo el problema del potencial.
En el caso de un sistema de dos conductores, el resultado es una relación lineal entre las cargas y los potenciales

Estos problemas se simplifican mucho mediante la construcción de circuitos equivalentes, donde cada par de superficies conductoras en influencia total se modela como un conductor.
3 Caso general
En este caso concreto, todas las superficies conductoras son esferas concéntricas. Dado que todas ellas son equipotenciales debemos preguntarnos qué distribución de carga produce un potencial uniforme sobre una esfera. La respuesta es sencilla: por la simetría del sistema, lo que tenemos son distribuciones de carga uniformes sobre cada superficie. Esto no sería cierto si tuviéramos esferas descentradas, por ejemplo.
Si las superficies esféricas están cargadas uniformemente, el problema es muy sencillo y ya ha sido resuelto en el tema de electrostática en el vacío. El potencial creado por una superficie cargada uniformemente es, para cualquier punto del espacio
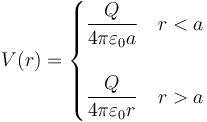
En este caso tenemos tres superficies cargadas. Una de radio a con una carga Qa (diferente en cada caso), una de radio b, que sería la de la cara interior de la corona, y una Qc en la esfera de radio c que sería la cara exterior.
La carga de cada conductor es la suma de las cargas de todas sus superficies, por lo que será

Por otro lado, de acuerdo con el teorema de Faraday, la carga en la pared del hueco será igual en magnitud a la encerrada en el hueco y de signo contrario.
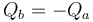
Por tanto

3.1 Potenciales en función de las cargas
Aplicando el resultado anterior tenemos,
3.1.1 Superficie de radio a
Para el potencial de la esfera maciza, tenemos una superficie que es coincidente de la de radio a, está en el interior de la de radio b y en el interior de la de radio c. Para las dos últimas el potencial es el correspondiente al interior de una superficie cargada y para la primera es indiferente que usemos el interior o el exterior, ya que ambos coinciden sobre la propia superficie.
El potencial de la superficie de radio a coincide con el potencial de toda la esfera maciza, que es el conductor 1.
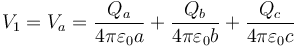
Sustituyendo las cargas en cada superficie
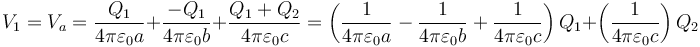
3.1.2 Superficie de radio b
Para la pared del hueco, tenemos una superficie que está fuera de la de radio a, coincidente con la de radio b y dentro de la de radio c. Aplicando el potencial correspondiente a cada caso queda
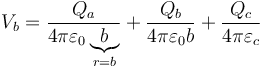
que da
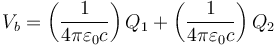
3.1.3 Superficie de radio c
Si consideramos la pared exterior de la corona esférica, tenemos ahora una que está fuera de la de radio a, fuera de la de radio b y coincidente con la de radio c, por lo que podemos aplicar el potencial exterior en cada caso
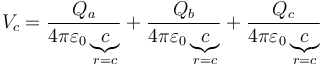
que da, de nuevo,
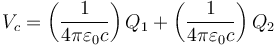
Este potencial es el mismo que el de la cara interior ya que ambas superficies pertenecen al mismo conductor. Es consecuencia del teorema de Faraday.
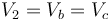
Numéricamente, en el SI,
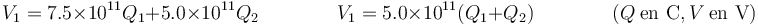
Si medimos la carga en nanoculombios y el voltaje en kilovoltios (como aparece en todos los apartados del enunciado) se simplifican los exponentes
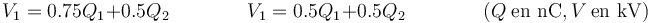
o en forma racional (aproximada, pues ke no vale exactamente 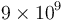 en el SI)
en el SI)
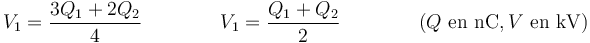
Estas relaciones pueden escribirse en forma matricial como
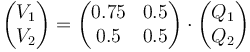
3.2 Cargas en función de los potenciales
A partir de los resultados anteriores, podemos despejar las cargas de los dos conductores en función de ambos potenciales. El resultado es
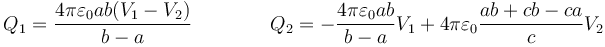
con los valores numéricos
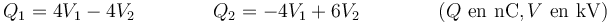
En forma matricial, el cálculo equivale a invertir la relación anterior
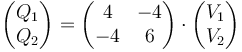
3.3 Circuito equivalente
Los sistemas de conductores se pueden analizar de forma alternativa mediante la construcción de un circuito equivalente de condensadores. Cada condensador representa aquellas superficies de los conductores que se encuentran en influencia total.
En este caso, tenemos dos nodos, uno por cada conductor. El circuito consta de dos condensadores. Uno representa a la superficie de la esfera maciza y a la cara interior de la corteza. Este condensador conecta los dos nodos. El valor de su capacidad es
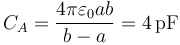
El otro representa aquellas líneas de campo que van de la superficie exterior de la corteza hacia el infinito. Su capacidad es igual a la de un conductor esférico
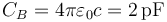
La carga de cada conductor es la suma de las cargas almacenadas en los condensadores unidos a los nodos correspondientes. Para el conductor 1, solo está el primer condensador
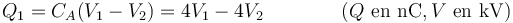
Para el conductor 2 tenemos dos condensadores unidos al nodo. Uno con d.d.p. entre placas V2 − V1 y otro con d.d.p. V2 − 0 (ya que el infinito está a tierra). Por tanto
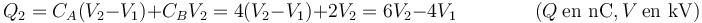
3.4 Energía electrostática
Una vez que se conoce la relación entre cargas y potenciales en el sistema, puede calcularse la energía electrostática que almacena, según la fórmula
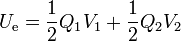
que se puede escribir como el producto de dos matrices
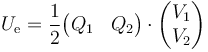
Si sustituimos aquí los potenciales en función de las cargas, usando como antes kilovoltios y nanoculombios para potenciales y cargas y dando el resultado en microjulios
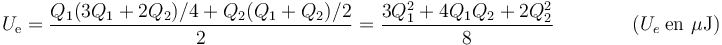
Matricialmente, este cálculo lo da la expresión
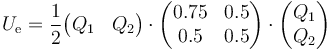
Alternativamente, podemos sustituir las cargas en función de los potenciales, empleando las mismas unidades que antes,
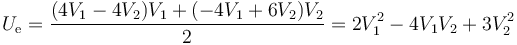
Esta energía también se puede escribir como suma de la almacenada en los diferentes condensadores
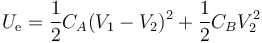
con el valor numérico, en las mismas unidades,
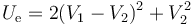
De esta última expresión, es evidente que la energía almacenada es siempre positiva.
4 Análisis de los diferentes casos
Armados con todas estas herramientas, ahora el cálculo se reduce a la sustitución en las diferentes ecuaciones. Sin embargo, la mayoría de las situaciones propuestas propiedades específicas o pueden ser objeto de confusión, por lo que conviene analizar los resultados.
4.1 Primer caso
En la primera situación, la corteza está aislada y descargada. Esto quiere decir que
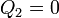
(no que su potencial es cero). También conocemos la carga de la esfera
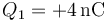
Sustituyendo obtenemos los potenciales, en kilovoltios

siendo la energía almacenada, en microjulios
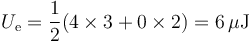
El que la corteza no esté cargada, no quiere decir que haya una carga nula en sus superficies. En la pared del hueco por el teorema de Faraday habrá −4 nC y, puesto que la carga total es nula, en la superficie exterior habrá +4 nC.
Empleando el circuito equivalente, al estar el conductor 2 aislado y descargado, el sistema se reduce a dos condensadores en serie, siendo la capacidad equivalente
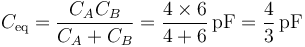
lo que da el voltaje para el conductor 1
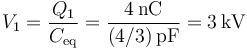
Para el conductor 2 hay que emplear que los condensadores están en serie y por tanto su carga es la misma, por lo que
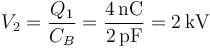
La energía almacenada, empleando el circuito, es
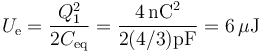
4.2 Segundo caso
En el segundo caso la esfera es la que está descargada, por lo que tenemos

Sustituyendo ahora en la expresión de los potenciales

Los dos conductores están al mismo potencial, ya que el único campo es el debido a la esfera exterior.
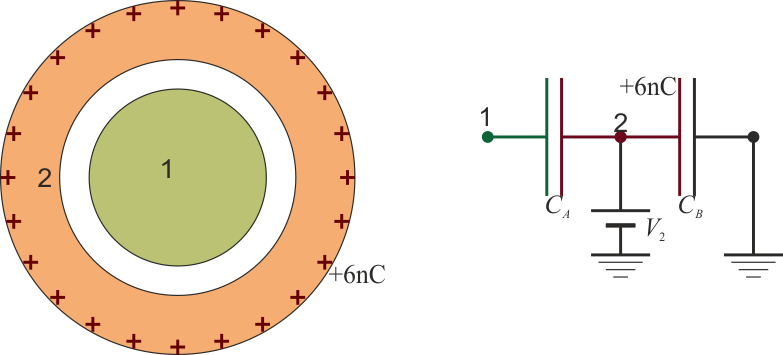
En este caso, toda la carga se encuentra en la superficie exterior y tanto la esfera como la parede del hueco están descargadas.
La energía almacenada es ahora
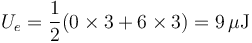
En el circuito equivalente, el condensador CA, al estar descargado, es como si no estuviera y el único fuera el CB
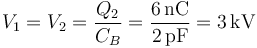
4.3 Tercer caso
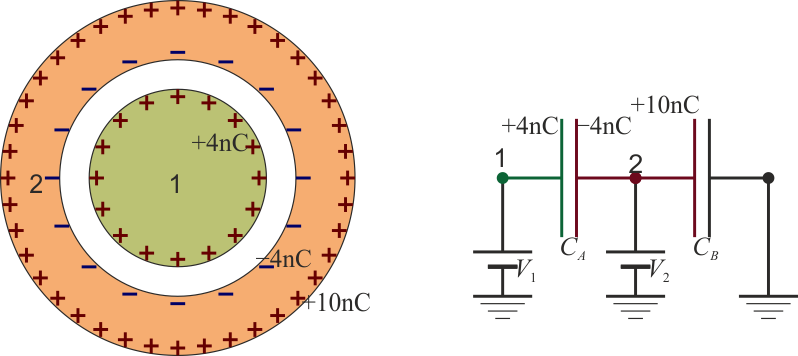
Cuando mantenemos la esfera con la misma carga que en el apartado anterior, pero además está cargada la corteza, cambian los potenciales de ambos conductores. Tenemos, como dato, las dos cargas

Sustituyendo en la expresión para los potenciales queda

Vemos que, como consecuencia de que las cargas sean la suma de las de los casos anteriores, también los potenciales lo son.
En este caso, habrá una carga de +4 nC es la esfera, de −4 nC en el hueco y 10 nC (6-(-4)) en la superficie exterior.
La energía en este caso es
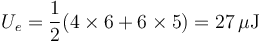
Comparando este resultado con los de los dos casos anteriores, vemos que la energía almacenada no es la suma de las de los dos casos individuales. Es decir, el potencial eléctrico sí cumple el principio de superposición, pero la energía electrostática no lo hace.
4.4 Cuarto caso
En el siguiente caso, tenemos las dos esferas cargas con cargas de la misma magnitud pero signo opuesto.

En este caso, los voltajes son
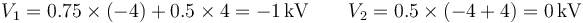
y la energía
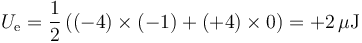
En este caso, toda la carga de la esfera exterior estará en la pared del hueco, quedando descargada la superficie exterior.
Desde el punto de vista del circuito, lo que ocurre en este caso es que, al estar el conductor 2 a tierra, el condensador B está descargado, por lo que toda la carga y la energía se almacenan en el A.
Nótese también que aunque la carga es negativa, la energía es positiva.
4.5 Quinto caso
En este caso tenemos también cargas opuestas, pero de distinta magnitud.

Sustituyendo en la expresión para los potenciales queda
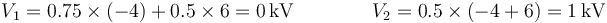
En este caso, las cargas son las del segundo apartado menos las del primero, y lo mismo ocurre con los potenciales.
La distribución de cargas es −4 C en la esfera, +4 nC en la pared del hueco y +2 nC en la superficie exterior. ´Notse que es perfectamente posible que las dos caras almacenen cargas del mismo signo. No tienen por qué ser de signo opuesto.
La energía en este caso
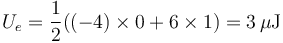
De nuevo, tenemos un caso que es combinación de los dos primeros (en este caso, la diferencia) y podemos comprobar cómo la energía no verifica el principio de superposición.
En este caso, al estar la esfera interior a tierra, el circuito equivale a dos condensadores puestos en paralelo, siendo su capacidad equivalente
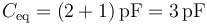
lo que da el potencial para la corteza
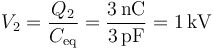
y da la energía almacenada
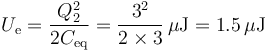
4.6 Sexto caso
Ahora cambian los datos que se dan. En el primer dato se decía que la esfera estaba aislada y descargada, lo cual equivale a que la carga era nula. Ahora está a tierra, lo que implica que su potencial es cero.

Obtenemos los datos que faltan despejando de las relaciones anteriores. Del potencial de la corteza

Al llegar a este punto podemos ver que ahora la situación exactamente la misma que en el cuarto caso, pero con el signo de las cargas invertido.
Por ello, los potenciales también cambian de signo
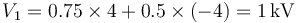
mientras que la energía del sistema mantiene su valor
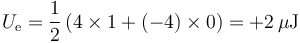
Como en el cuarto caso, el circuito equivalente se reduce a solo el condensador A, por estar el Bcon sus placas al mismo potencial.
Las cargas y potenciales tienen signo opuesto a las de ese caso, pero la energía almacenada vale lo mismo.
4.7 Séptimo caso
Ahora es la esfera interior la que está a tierra.

Operamos del mismo modo y obtenemos

Por este resultado vemos que este caso es exactamente el mismo que el 5º, por lo que

El circuito equivalente en este caso es, como dijimos antes, uno formado por dos condensadores en paralelo.
4.8 Octavo caso
Ahora conocemos los potenciales de los dos conductores,

por lo que empleamos las ecuaciones para las cargas en función de los potenciales. Para la esfera
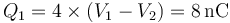
y para la corona
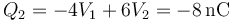
Podemos ver que este caso es igual al cuarto multiplicado por -2, solo que allí el dato eran las cargas y aquí los voltajes.
La energía almacenada es entonces el cuádruple (2²) de la del cuarto caso
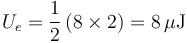
4.9 Noveno caso
Operando como en el caso anterior

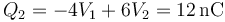
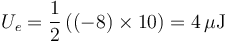
4.10 Décimo caso
Si las dos están al mismo potencial
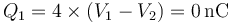
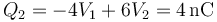
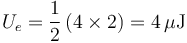
4.11 Undécimo caso
Por último