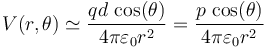Entrar Página Discusión Historial Go to the site toolbox

Dipolo eléctrico (GIE)

De Laplace

(Diferencias entre revisiones)
Línea 30: Línea 30:
==Efecto de un campo externo uniforme sobre un dipolo==
==Efecto de un campo externo uniforme sobre un dipolo==
 +
Si un dipolo se encuentra inmerso en un campo eléctrico uniforme, <math>\vec{E}_0</math>, aparecen sobre él dos fuerzas: una sobre la carga positiva y otra sobre la negativa (más si hay más de dos cargas, como en el caso del agua).
 +
 +
Por ser nula la carga neta se anula la resultante de las fuerzas externas sobre el dipolo
 +
 +
<center><math>\vec{F}=\vec{F}_++\vec{F}_- = (+q)\vec{E}_0+(-q)\vec{E}_0=(q-q)\vec{E}_0=\vec{0}</math></center>
 +
 +
Esto implica que, tal como se ve al estudiar la dinámica del sólido rígido, el CM del dipolo no tiende a moverse.
 +
 +
Sin embargo, sí que aparece un par de fuerzas, ya que las fuerzas no están aplicadas sobre la misma recta soporte. El momento del par vale
 +
 +
<center><math>\vec{M}=\vec{r}_+\times\vec{F}_++\vec{r}_-\times\vec{F}_-=q(\vec{r}_+-\vec{r}_-)\times\vec{E}_0=\vec{p}\times\vec{E}_0</math></center>
 +
 +
Esta expresión se verifica también para distribuciones dipolares más complejas, como la de la molécula de agua. Para todas ellas
 +
 +
<center><math>\vec{M}=\vec{p}\times\vec{E}_0</math></center>
 +
 +
El efecto de este par de fuerzas es girar el dipolo tendiendo a alinearlo con el campo eléctrico. Es el mismo principio que, en el campo magnético, explica el funcionamiento de una brújula.
 +
==Potencial y campo debido a un dipolo==
==Potencial y campo debido a un dipolo==
 +
Un dipolo, además de experimentar los efectos de un campo externo, también genera un campo propio.
 +
 +
===Potencial eléctrico===
 +
Supongamos un dipolo formado por dos cargas puntuales situadas en <math>\pm(d/2)\vec{k}</math>. El potencial eléctrico, en un punto <math>\vec{r}</math> del espacio, debido a estas dos cargas será
 +
 +
<center><math>V(\vec{r})=\frac{1}{4\pi\varepsilon_0}\left(\frac{q}{|\vec{r}-(d/2)\vec{k}|}-\frac{q}{|\vec{r}+(d/2)\vec{k}|}\right)</math></center>
 +
 +
Empleando el teorema del coseno estas distancias se pueden escribir como
 +
 +
<center><math>\left|\vec{r}\pm \frac{d}{2}\vec{k}\right| = \sqrt{r^2\pm dr\cos(\theta)+\frac{d^2}{4}}</math></center>
 +
 +
siendo <math>\theta</math> el ángulo que el vector <math>\vec{r}</math> forma con el eje OZ. Llevando esto al potencial
 +
 +
<center><math>V(\vec{r})=\frac{1}{4\pi\varepsilon_0}\left(\frac{q}{\sqrt{r^2-dr\,\cos(\theta)+d^2/4}}-\frac{q}{\sqrt{r^2+dr\,\cos(\theta)+d^2/4}}\right)</math></center>
 +
 +
En la mayoría de las situaciones, el potencial y el campo del dipolo interesan a grandes distancias de éstos (comparadas con el tamaño del propio dipolo). Por ejemplo, una molécula de agua mide unos cuantos nanómetros. Una distancia de solo 1mm ya es un millón de veces más grande que el tamaño del dipolo. En ese caso, podemos hacer uso del desarrollo del binomio de Newton
 +
 +
<center><math>(1+\epsilon)^n\simeq 1 + n\epsilon+ \cdots</math></center>
 +
 +
que para el caso <math>n = -1/2</math> nos permite reducir la expresión anterior a
 +
 +
<center><math>V(r,\theta)\simeq\frac{qd\,\cos(\theta)}{4\pi\varepsilon_0 r^2}=\frac{p\,\cos(\theta)}{4\pi\varepsilon_0 r^2}</math></center>
 +
[[Categoría:Electrostática en el vacío (GIE)]]
[[Categoría:Electrostática en el vacío (GIE)]]

Revisión de 15:26 4 abr 2015

Contenido

1 Definición. Momento dipolar

En su versión más sencilla, un dipolo es un sistema formado por dos cargas de la misma magnitud y signo opuesto, separadas una cierta distancia.

Más en general, un sistema neutro pero en el que el centro de las cargas positivas no coincide con el de las negativas también se conoce como un dipolo. Un ejemplo típico es la molécula de agua. Al ser el oxígeno más electronegativo que el hidrógeno, se produce una acumulación de carga negativa en el lado en que se halla el oxígeno, y de carga positiva en el opuesto.

No todas las moléculas poseen momento dipolar. El dióxido de carbono, por ejemplo, es una mole´cula simétrica que no tiene momento dipolar neto ya que el centro de las cargas positivas y el de las cargas negativas es el mismo.

El dipolo se caracteriza matemáticamente por su momento dipolar, que para dos cargas puntuales se define como

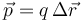
\vec{p}=q\,\Delta\vec{r}

siendo 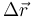\Delta\vec{r} el vector de posición relativa que va de la carga negativa a la positiva.

Esta expresión se generaliza fácilmente a una distribución arbitraria observando que equivale a

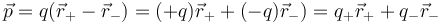
\vec{p}=q(\vec{r}_{+}-\vec{r}_{-})=(+q)\vec{r}_{+}+(-q)\vec{r}_{-})=q_{+}\vec{r}_{+}+q_{-}\vec{r}_{-}

Y de aquí pasamos a una distribución de cargas puntuales

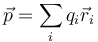
\vec{p}=\sum_iq_i\vec{r}_i

y a una dustribución volumétrica, superficial o lineal

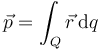
\vec{p}=\int_Q \vec{r}\,\mathrm{d}q

El momento dipolar es una magnitud vectorial cuya unidad en el SI es el culombio·metro.

2 Efecto de un campo externo uniforme sobre un dipolo

Si un dipolo se encuentra inmerso en un campo eléctrico uniforme, 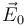\vec{E}_0, aparecen sobre él dos fuerzas: una sobre la carga positiva y otra sobre la negativa (más si hay más de dos cargas, como en el caso del agua).

Por ser nula la carga neta se anula la resultante de las fuerzas externas sobre el dipolo

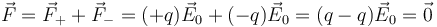
\vec{F}=\vec{F}_++\vec{F}_- = (+q)\vec{E}_0+(-q)\vec{E}_0=(q-q)\vec{E}_0=\vec{0}

Esto implica que, tal como se ve al estudiar la dinámica del sólido rígido, el CM del dipolo no tiende a moverse.

Sin embargo, sí que aparece un par de fuerzas, ya que las fuerzas no están aplicadas sobre la misma recta soporte. El momento del par vale

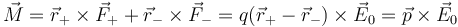
\vec{M}=\vec{r}_+\times\vec{F}_++\vec{r}_-\times\vec{F}_-=q(\vec{r}_+-\vec{r}_-)\times\vec{E}_0=\vec{p}\times\vec{E}_0

Esta expresión se verifica también para distribuciones dipolares más complejas, como la de la molécula de agua. Para todas ellas

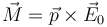
\vec{M}=\vec{p}\times\vec{E}_0

El efecto de este par de fuerzas es girar el dipolo tendiendo a alinearlo con el campo eléctrico. Es el mismo principio que, en el campo magnético, explica el funcionamiento de una brújula.

3 Potencial y campo debido a un dipolo

Un dipolo, además de experimentar los efectos de un campo externo, también genera un campo propio.

3.1 Potencial eléctrico

Supongamos un dipolo formado por dos cargas puntuales situadas en 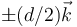\pm(d/2)\vec{k}. El potencial eléctrico, en un punto \vec{r} del espacio, debido a estas dos cargas será

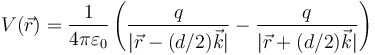
V(\vec{r})=\frac{1}{4\pi\varepsilon_0}\left(\frac{q}{|\vec{r}-(d/2)\vec{k}|}-\frac{q}{|\vec{r}+(d/2)\vec{k}|}\right)

Empleando el teorema del coseno estas distancias se pueden escribir como

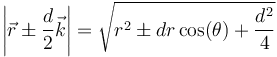
\left|\vec{r}\pm \frac{d}{2}\vec{k}\right| = \sqrt{r^2\pm dr\cos(\theta)+\frac{d^2}{4}}

siendo θ el ángulo que el vector \vec{r} forma con el eje OZ. Llevando esto al potencial

V(\vec{r})=\frac{1}{4\pi\varepsilon_0}\left(\frac{q}{\sqrt{r^2-dr\,\cos(\theta)+d^2/4}}-\frac{q}{\sqrt{r^2+dr\,\cos(\theta)+d^2/4}}\right)

En la mayoría de las situaciones, el potencial y el campo del dipolo interesan a grandes distancias de éstos (comparadas con el tamaño del propio dipolo). Por ejemplo, una molécula de agua mide unos cuantos nanómetros. Una distancia de solo 1mm ya es un millón de veces más grande que el tamaño del dipolo. En ese caso, podemos hacer uso del desarrollo del binomio de Newton

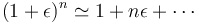
(1+\epsilon)^n\simeq 1 + n\epsilon+ \cdots

que para el caso n = − 1 / 2 nos permite reducir la expresión anterior a

V(r,\theta)\simeq\frac{qd\,\cos(\theta)}{4\pi\varepsilon_0 r^2}=\frac{p\,\cos(\theta)}{4\pi\varepsilon_0 r^2}
Obtenido de "http://tesla.us.es/wiki/index.php/Dipolo_el%C3%A9ctrico_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace