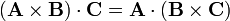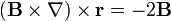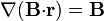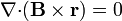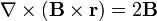Entrar Página Discusión Historial Go to the site toolbox

Algunas identidades vectoriales

De Laplace

(Diferencias entre revisiones)
(→<math>(\mathbf{B}{\cdot}\nabla)\mathbf{r}=\mathbf{B}</math>)
(→<math>(\mathbf{B}\times\nabla){\cdot}\mathbf{r}=0</math>)
Línea 33: Línea 33:
===<math>(\mathbf{B}\times\nabla){\cdot}\mathbf{r}=0</math>===
===<math>(\mathbf{B}\times\nabla){\cdot}\mathbf{r}=0</math>===
 +
Este se puede hacer directamente observando que <math>\nabla</math> es un operador vectorial y, por tanto, siempre que no se cambie el orden de los términos y se tenga claro sobre qué actúa, pueden aplicarse las fórmulas del álgebra vectorial. En particular, puede aplicarse la propiedad del producto mixto
 +
 +
<center><math>\left(\mathbf{A}\times\mathbf{B}\right)\cdot\mathbf{C}=\mathbf{A}\cdot\left(\mathbf{B}\times\mathbf{C}\right)</math></center>
[[Categoría:Problemas de fundamentos matemáticos]]
[[Categoría:Problemas de fundamentos matemáticos]]

Revisión de 09:41 22 dic 2008

Contenido

1 Enunciado

Demuestre que si \mathbf{r} es el vector de posición y \mathbf{B} un campo vectorial arbitrario

  1. (\mathbf{B}{\cdot}\nabla)\mathbf{r}=\mathbf{B}
  2. (\mathbf{B}\times\nabla){\cdot}\mathbf{r}=0
  3. (\mathbf{B}\times\nabla)\times\mathbf{r}=-2\mathbf{B}

Igualmente, para el caso particular en que \mathbf{B} represente un vector constante, demuestre que

  1. \nabla(\mathbf{B}{\cdot}\mathbf{r})=\mathbf{B}
  2. \nabla{\cdot}(\mathbf{B}\times\mathbf{r})=0
  3. \nabla\times(\mathbf{B}\times\mathbf{r})=2\mathbf{B}

2 Solución

2.1 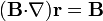(\mathbf{B}{\cdot}\nabla)\mathbf{r}=\mathbf{B}

El operador escalar 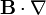\mathbf{B}\cdot\nabla se expresa, en cartesianas, como

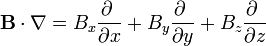
\mathbf{B}\cdot\nabla = B_x\frac{\partial\ }{\partial x}+B_y\frac{\partial\ }{\partial y}+B_z\frac{\partial\ }{\partial z}

Cuando este operador actúa sobre un campo vectorial, el resultado es la suma de nueve términos, ya que hay que “multiplicar” este operador vectorial por cada una de las componentes del campo vectorial sobre el que actúa:

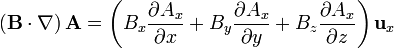
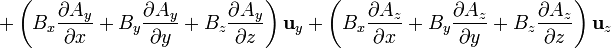
\left(\mathbf{B}\cdot\nabla\right)\mathbf{A}= \left(B_x\frac{\partial A_x}{\partial x}+B_y\frac{\partial A_x}{\partial y}+B_z\frac{\partial A_x}{\partial z}\right)\mathbf{u}_x+\left(B_x\frac{\partial A_y}{\partial x}+B_y\frac{\partial A_y}{\partial y}+B_z\frac{\partial A_y}{\partial z}\right)\mathbf{u}_y+ \left(B_x\frac{\partial A_z}{\partial x}+B_y\frac{\partial A_z}{\partial y}+B_z\frac{\partial A_z}{\partial z}\right)\mathbf{u}_z

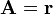Cuando \mathbf{A}=\mathbf{r} esta expresión se simplifica notablemente, ya que

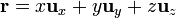
\mathbf{r}=x\mathbf{u}_x + y\mathbf{u}_y+z\mathbf{u}_z

y queda

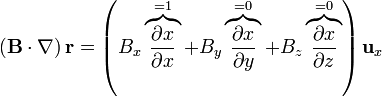
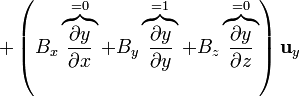
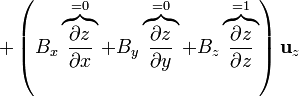
\left(\mathbf{B}\cdot\nabla\right)\mathbf{r}= \left(B_x\overbrace{\frac{\partial x}{\partial x}}^{=1}+B_y\overbrace{\frac{\partial x}{\partial y}}^{=0}+B_z\overbrace{\frac{\partial x}{\partial z}}^{=0}\right)\mathbf{u}_x+\left(B_x\overbrace{\frac{\partial y}{\partial x}}^{=0}+B_y\overbrace{\frac{\partial y}{\partial y}}^{=1}+B_z\overbrace{\frac{\partial y}{\partial z}}^{=0}\right)\mathbf{u}_y+ \left(B_x\overbrace{\frac{\partial z}{\partial x}}^{=0}+B_y\overbrace{\frac{\partial z}{\partial y}}^{=0}+B_z\overbrace{\frac{\partial z}{\partial z}}^{=1}\right)\mathbf{u}_z=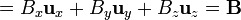B_x\mathbf{u}_x+B_y\mathbf{u}_y+B_z\mathbf{u}_z=\mathbf{B}

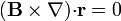
2.2 (\mathbf{B}\times\nabla){\cdot}\mathbf{r}=0

Este se puede hacer directamente observando que \nabla es un operador vectorial y, por tanto, siempre que no se cambie el orden de los términos y se tenga claro sobre qué actúa, pueden aplicarse las fórmulas del álgebra vectorial. En particular, puede aplicarse la propiedad del producto mixto

\left(\mathbf{A}\times\mathbf{B}\right)\cdot\mathbf{C}=\mathbf{A}\cdot\left(\mathbf{B}\times\mathbf{C}\right)
Obtenido de "http://tesla.us.es/wiki/index.php/Algunas_identidades_vectoriales"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace