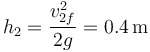Entrar Página Discusión Historial Go to the site toolbox

Colisión en el interior de un cuenco

De Laplace

(Diferencias entre revisiones)
Línea 34: Línea 34:
La componente radial de esta ecuación vectorial es la normal al desplazamiento. Por tanto, tenemos
La componente radial de esta ecuación vectorial es la normal al desplazamiento. Por tanto, tenemos
-
<center><math>m_1\frac{|\vec{v}_1|^2}{R} = -mg +F_n</math></center>
+
<center><math>m_1\frac{|\vec{v}_1|^2}{R} = -m_1g +F_n</math></center>
Despejamos la fuerza y sustituimos el valor de la rapidez calculado anteriormente.
Despejamos la fuerza y sustituimos el valor de la rapidez calculado anteriormente.
-
<center><math>F_n = mg + m\frac{v_B^2}{R}= 3mg = 29.4\,\mathrm{N}</math></center>
+
<center><math>F_n = m_1g + m_1\frac{v_B^2}{R}= 3m_1g = 29.4\,\mathrm{N}</math></center>
La fuerza normal en este punto es el triple del peso de la masa.
La fuerza normal en este punto es el triple del peso de la masa.
 +
==Velocidades tras el impacto==
==Velocidades tras el impacto==
 +
En el impacto tenemos una colisión elástica, en la que se conserva la cantidad de movimiento. Considerando solo la componente horizontal (única no nula)
 +
 +
<center><math>m_1v_1 + m_2\cdot 0=m_1v_{1f}+m_2v_{2f}</math></center>
 +
 +
y el coeficiente de restitución es igual a la unidad
 +
 +
<center><math>v_{2f}-v_{1f}=v_{1i}-v_{2i}= v_1\,</math></center>
 +
 +
La solución de este sistema lineal es
 +
 +
<center><math>v_{1f}=\frac{m_1-m_2}{m_1+m_2}v_1\qquad\qquad v_{2f}=\frac{2m_1}{m_1+m_2}v_1</math></center>
 +
 +
con valor numérico
 +
 +
<center><math>v_{1f}=-4.2\,\frac{\mathrm{m}}{\mathrm{s}}\qquad\qquad v_{2f}=2.8\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
 +
 +
La partícula ligera rebota, mientras que la pesada sale hacia adelante con una velocidad más pequeña.
 +
==Alturas máximas==
==Alturas máximas==
 +
Aplicando de nuevo la ley de conservación de la energía mecánica obtenemos las alturas máximas alcanzadas por cada partícula.
 +
 +
Para la partícula de 1&thinsp;kg
 +
 +
<center><math>m_1gh_1 = \frac{1}{2}mv_{1f}^2\qquad\Rightarrow\qquad h_1=\frac{v_{1f}^2}{2g}=0.9\,\mathrm{m}</math></center>
 +
 +
y para la de 4&thinsp;kg
 +
 +
<center><math>h_2 = \frac{v_{2f}^2}{2g}=0.4\,\mathrm{m}</math></center>
==Choque completamente inelástico==
==Choque completamente inelástico==
===Velocidad tras la colisión===
===Velocidad tras la colisión===

Revisión de 21:24 7 dic 2014

Contenido

1 Enunciado

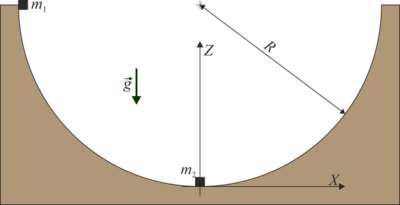
En el interior de un cuenco hemisférico de radio 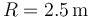R = 2.5\,\mathrm{m} cuyo borde es horizontal, se encuentran dos partículas que pueden deslizar sin rozamiento por su superficie. Una de ellas, de masa 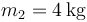m_2 = 4\,\mathrm{kg}, se encuentra en reposo en el fondo del cuenco. La otra, de masa 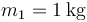m_1 = 1\,\mathrm{kg} se coloca en el borde del cuenco y desde allí se suelta.

  1. Calcule, con justificación, la velocidad que lleva la masa 1 justo antes de impactar con la masa 2. Halle la reacción del cuenco sobre la masa 1 para el mismo instante.
  2. Si el choque es perfectamente elástico, calcule las velocidades de las dos masas justo tras la colisión.
  3. Para este caso elástico, halle la altura máxima desde el fondo del cuenco que alcanza cada una de las masas tras el choque.
  4. Repita los dos apartados anteriores para el caso de que la colisión sea completamente inelástica. ¿Cuánta energía se pierde en la colisión en ese caso?

Tómese g = 9.8m/s²

2 Velocidad antes del impacto

Las fuerzas que actúan sobre la masa 1 en su descenso son el peso y la reacción normal del cuenco. Esta última, al ser perpendicular al desplazamiento, no realiza trabajo sobre la partícula. Por ello, se cumple la ley de conservación de la energía mecánica

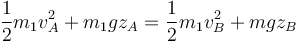
\frac{1}{2}m_1v_A^2+m_1gz_A = \frac{1}{2}m_1v_B^2+mgz_B

Tomando como altura de referencia el fondo del cuenco y aplicando que la velocidad inicial es nula, esta ley se reduce a

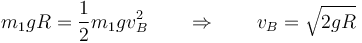
m_1gR = \frac{1}{2}m_1gv_B^2\qquad\Rightarrow\qquad v_B = \sqrt{2gR}

que tiene el valor numérico

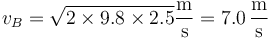
v_B = \sqrt{2\times 9.8\times 2.5}\frac{\mathrm{m}}{\mathrm{s}} = 7.0\,\frac{\mathrm{m}}{\mathrm{s}}

En forma vectorial

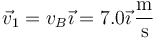
\vec{v}_1 = v_B\vec{\imath}=7.0\vec{\imath}\,\frac{\mathrm{m}}{\mathrm{s}}

La reacción del fondo la hallamos observando que la segunda ley en ese punto nos da

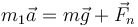
m_1\vec{a}=m\vec{g}+\vec{F}_n

La componente radial de esta ecuación vectorial es la normal al desplazamiento. Por tanto, tenemos

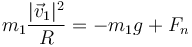
m_1\frac{|\vec{v}_1|^2}{R} = -m_1g +F_n

Despejamos la fuerza y sustituimos el valor de la rapidez calculado anteriormente.

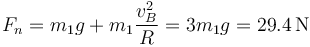
F_n = m_1g + m_1\frac{v_B^2}{R}= 3m_1g = 29.4\,\mathrm{N}

La fuerza normal en este punto es el triple del peso de la masa.

3 Velocidades tras el impacto

En el impacto tenemos una colisión elástica, en la que se conserva la cantidad de movimiento. Considerando solo la componente horizontal (única no nula)

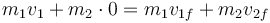
m_1v_1 + m_2\cdot 0=m_1v_{1f}+m_2v_{2f}

y el coeficiente de restitución es igual a la unidad

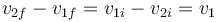
v_{2f}-v_{1f}=v_{1i}-v_{2i}= v_1\,

La solución de este sistema lineal es

v_{1f}=\frac{m_1-m_2}{m_1+m_2}v_1\qquad\qquad v_{2f}=\frac{2m_1}{m_1+m_2}v_1

con valor numérico

v_{1f}=-4.2\,\frac{\mathrm{m}}{\mathrm{s}}\qquad\qquad v_{2f}=2.8\,\frac{\mathrm{m}}{\mathrm{s}}

La partícula ligera rebota, mientras que la pesada sale hacia adelante con una velocidad más pequeña.

4 Alturas máximas

Aplicando de nuevo la ley de conservación de la energía mecánica obtenemos las alturas máximas alcanzadas por cada partícula.

Para la partícula de 1 kg

m_1gh_1 = \frac{1}{2}mv_{1f}^2\qquad\Rightarrow\qquad h_1=\frac{v_{1f}^2}{2g}=0.9\,\mathrm{m}

y para la de 4 kg

h_2 = \frac{v_{2f}^2}{2g}=0.4\,\mathrm{m}

5 Choque completamente inelástico

5.1 Velocidad tras la colisión

5.2 Altura máxima

5.3 Balance energético

Obtenido de "http://tesla.us.es/wiki/index.php/Colisi%C3%B3n_en_el_interior_de_un_cuenco"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace