Osciladores no lineales. Péndulo simple (GIE)
De Laplace
| Línea 57: | Línea 57: | ||
==Oscilador no lineal== | ==Oscilador no lineal== | ||
| + | El anterior análisis posee aplicabilidad directa, pero además es extremadamente útil como primera aproximación a sistemas más complejos (incluyendo una descripción más detallada de los medios elásticos). | ||
| + | |||
===Posiciones de equilibrio=== | ===Posiciones de equilibrio=== | ||
| + | Siguiendo con el caso de un movimiento unidimensional, si tenemos una partícula sometida a una fuerza dependiente de la posición, se cumplirá | ||
| + | |||
| + | <center><math>m\ddot{x}=F(x)</math></center> | ||
| + | |||
| + | Los puntos de equilibrio serán aquellos en que si se deposita en ellos la partícula en reposo, ésta no abandona la posición. La condición para ello es que la aceleración sea nula. Por tanto los puntos de equilibrio son aquellos en que se anula la fuerza | ||
| + | |||
| + | <center><math>F(x_0) = 0 \qquad\Rightarrow\qquad x_0</math> es un punto de equilibrio</center> | ||
===Aproximación lineal y parabólica=== | ===Aproximación lineal y parabólica=== | ||
===Frecuencia aproximada=== | ===Frecuencia aproximada=== | ||
Revisión de 18:03 23 nov 2014
Contenido |
1 Oscilaciones lineales. El oscilador armónico
El oscilador armónico es un modelo teórico que se aplica en primer lugar al comportamiento de sólidos elásticos, que verifican la ley de Hooke, pero cuya validez se extiende a muchísimos otros sistemas mecánicos (y físicos, en general, ya que es esencial en la teoría de circuitos en los campos electromagnéticos). La razón de su universalidad es que se trata del oscilador más sencillo posible: aquél en que la fuerza es lineal con la posición.
1.1 Ley de Hooke
Restringiéndonos al caso unidimensional, la ley de Hppke nos dice que la fuerza producida por un resorte elástico sobre una partícula es de la forma

siendo xeq la posición de equilibrio para la cual esta fuerza es nula.
La ley de Hooke describe una fuerza recuperadora:
- cuando x > xeq, la fuerza es negativa, lo cual quiere decir que tiende a reducir x.
- cuando x < xeq, la fuerza es positiva, es decir, tiende a aumentar x.
Gráficamente, si representamos la fuerza como función de la longitud del resorte, el resultado es una recta de pendiente − k, es decir,
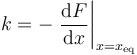
Esta recta pasa por F = 0 en la posición de equilibrio.
1.2 Energía potencial
Al tratarse de una fuerza en una dimensión y dependiente de la posición, deriva de una energía potencial según la relación
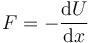
lo que da para este caso
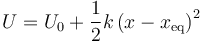
siendo U0 una constante, que depende del origen de potencial elegido.
Gráficamente, la curva de energía potencial es una parábola con un mínimo en la posición de equilibrio. Se trata de un mínimo porque la segunda derivada es positiva

Para el oscilador armónico sin rozamiento se cumple la conservación de la energía mec´nica
que gráficamente corresponde a que la parábola se corta por una recta horizontal a la altura de la energía. Los puntos de corte de la recta con la parábola son los puntos de retorno, en los cuales la velocidad se anula.
1.3 Frecuencia de las oscilaciones
La segunda ley de Newton para el oscilador armónico
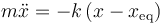
predice un comportamiento oscilatorio alrededor de la posición de equilibrio

siendo la frecuencia y el periodo de las oscilaciones

La amplitud de las oscilaciones es la máxima diferencia respecto a la posición de equilibrio, equivale a la mitad de la distancia entre los dos puntos de retorno.
2 Oscilador no lineal
El anterior análisis posee aplicabilidad directa, pero además es extremadamente útil como primera aproximación a sistemas más complejos (incluyendo una descripción más detallada de los medios elásticos).
2.1 Posiciones de equilibrio
Siguiendo con el caso de un movimiento unidimensional, si tenemos una partícula sometida a una fuerza dependiente de la posición, se cumplirá
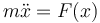
Los puntos de equilibrio serán aquellos en que si se deposita en ellos la partícula en reposo, ésta no abandona la posición. La condición para ello es que la aceleración sea nula. Por tanto los puntos de equilibrio son aquellos en que se anula la fuerza
 es un punto de equilibrio
es un punto de equilibrio




