Tabla de fórmulas de variable compleja
De Laplace
| Línea 2: | Línea 2: | ||
Se define la raíz cuadrada de -1 como la unidad imaginaria | Se define la raíz cuadrada de -1 como la unidad imaginaria | ||
| - | <center><math>i = j = \sqrt{-1}</math></center> | + | <center><math>\mathrm{i} = \mathrm{j} = \sqrt{-1}</math></center> |
En matemáticas se suele representar como i. En ingeniería como j para evitar confusiones con la intensidad de corriente. | En matemáticas se suele representar como i. En ingeniería como j para evitar confusiones con la intensidad de corriente. | ||
| Línea 62: | Línea 62: | ||
En la forma polar, el conjugado tiene el mismo módulo y argumento opuesto | En la forma polar, el conjugado tiene el mismo módulo y argumento opuesto | ||
| - | <center><math>\left|z^*\right| = \left|z\right|</math></center> | + | <center><math>\left|z^*\right| = \left|z\right|\qquad\qquad\arg(z^*)=-\arg(z)</math></center> |
| - | <center><math>\ | + | ===Cálculo de la parte real y parte imaginaria=== |
| + | Si conocemos un complejo y su conjugado, la parte real y la imaginaria pueden calcularse como | ||
| + | |||
| + | <center><math>\mathrm{Re}(z)=\frac{z+z^*}{2}\qquad\qquad \mathrm{Im}(z)=\frac{z-z^*}{2\mathrm{j}</math></center> | ||
| + | |||
| + | ===Cálculo del módulo === | ||
| + | A partir del complejo y su conjugado | ||
| + | |||
| + | <center><math>|z| = \sqrt{zz^*}</math></center> | ||
| + | |||
| + | ==Igualdad de complejos== | ||
| + | Dos complejos son iguales cuando son iguales sus partes reales y sus partes imaginarias | ||
| + | |||
| + | <center><math>z = w \Leftrightarrow \left\begin{array}{rcl}\mathrm{Re}(z)& = & \mathrm{Re}(w)\\ \mathrm{Im}(z)&=&\mathrm{Im}(w)\end{array}\right.</math></center> | ||
| + | |||
| + | En términos de módulo y argumento, son iguales cuando tienen el mismo módulo y su argumento se diferencia en un número entero de vueltas | ||
| + | |||
| + | <center><math>z = w \Leftrightarrow \left\begin{array}{rcl}|z|& = & |w|\\ \mathrm{arg}(z)&=&\mathrm{arg}(w)+2k\pi\end{array}\right.</math></center> | ||
| + | |||
| + | ==Suma de números complejos== | ||
| + | Para sumar dos complejos se suman sus partes reales y sus partes imaginarias | ||
| + | ==Producto de números complejos== | ||
| + | ==Fórmula de Euler== | ||
| + | ==Exponencial de un número complejo== | ||
| + | ==Logaritmo de un número complejo== | ||
| + | ==Funciones trigonométricas== | ||
| + | ==Funciones hiperbólicas== | ||
Revisión de 20:44 17 oct 2014
1 Unidad imaginaria
Se define la raíz cuadrada de -1 como la unidad imaginaria
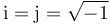
En matemáticas se suele representar como i. En ingeniería como j para evitar confusiones con la intensidad de corriente.
Con ayuda de la unidad imaginaria se puede clacular la raíz de cualquier número negativo
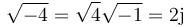
2 Números complejos
Se definen a partir de un par de números reales como
Los números complejos tienen numerosas similitudes con los pares de R2 (x,y) pero con propiedades adicionales.
2.1 Parte real y parte imaginaria
Para un número complejo de la forma anterior
- Parte real
- Es el sumando que no multiplica a la unidad imaginaria
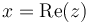
- Parte imaginaria
- Es el coeficiente que multiplica a la unidad imaginaria.
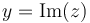
2.2 Representación en el plano complejo
Un número complejo puede representarse como un punto P(x,y) en un plano (denominado plano complejo). La parte real es la abcisa y la imaginaria la ordenada. El eje real es el conjunto de todos los complejos puramente reales y el eje imaginario el de todos los imaginarios puros.
Alternativamente, en lugar de un punto puede usarse un vector (llamado afijo) que une el origen z = 0 con el punto P(x,y) del plano.
2.3 Forma polar de un número complejo
Alternativamente, un número complejo puede representarse por su módulo (el del afijo)
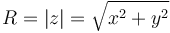
y su argumento, que es el ángulo que el afijo forma con el eje real
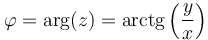
Las relaciones inversas de estas son

Existen distintas formas de expresar un número complejo en forma polar, una de ellas es
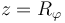
así
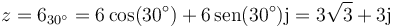
3 Conjugado de un número complejo
A partir de un número complejo z = x + yj se dfine su conjugado
es decir, con la misma parte real y con la parte imaginaria cambiada de signo.
Gráficamente el punto z * es el simétrico de z respecto al eje real.
En la forma polar, el conjugado tiene el mismo módulo y argumento opuesto
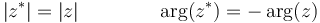
3.1 Cálculo de la parte real y parte imaginaria
Si conocemos un complejo y su conjugado, la parte real y la imaginaria pueden calcularse como
3.2 Cálculo del módulo
A partir del complejo y su conjugado
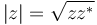
4 Igualdad de complejos
Dos complejos son iguales cuando son iguales sus partes reales y sus partes imaginarias
En términos de módulo y argumento, son iguales cuando tienen el mismo módulo y su argumento se diferencia en un número entero de vueltas
5 Suma de números complejos
Para sumar dos complejos se suman sus partes reales y sus partes imaginarias





