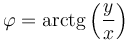Tabla de fórmulas de variable compleja
De Laplace
(Página creada con '==Unidad imaginaria== Se define la raíz cuadrada de -1 como la unidad imaginaria <center><math>i = j = \sqrt{-1}</math></center> En matemáticas se suele representar como u. …') |
|||
| Línea 4: | Línea 4: | ||
<center><math>i = j = \sqrt{-1}</math></center> | <center><math>i = j = \sqrt{-1}</math></center> | ||
| - | En matemáticas se suele representar como | + | En matemáticas se suele representar como i. En ingeniería como j para evitar confusiones con la intensidad de corriente. |
| + | |||
| + | Con ayuda de la unidad imaginaria se puede clacular la raíz de cualquier número negativo | ||
| + | |||
| + | <center><math>\sqrt{-4}=\sqrt{4}\sqrt{-1}=2\mathrm{j}</math></center> | ||
| + | ==Números complejos== | ||
| + | Se definen a partir de un par de números reales como | ||
| + | |||
| + | <center><math>z = x + y\mathrm{j}</math></center> | ||
| + | |||
| + | Los números complejos tienen numerosas similitudes con los pares de <math>R^2</math> <math>(x,y)</math> pero con propiedades adicionales. | ||
| + | |||
| + | ===Parte real y parte imaginaria=== | ||
| + | Para un número complejo de la forma anterior | ||
| + | |||
| + | ;Parte real: Es el sumando que no multiplica a la unidad imaginaria | ||
| + | <center><math>x = \mathrm{Re}(z)</math></center> | ||
| + | |||
| + | ;Parte imaginaria: Es el coeficiente que multiplica a la unidad imaginaria. | ||
| + | <center><math>y = \mathrm{Im}(z)</math></center> | ||
| + | |||
| + | ===Representación en el plano complejo=== | ||
| + | Un número complejo puede representarse como un punto <math>P(x,y)</math> en un plano (denominado ''plano complejo''). La parte real es la abcisa y la imaginaria la ordenada. El eje real es el conjunto de todos los complejos puramente reales y el eje imaginario el de todos los imaginarios puros. | ||
| + | |||
| + | Alternativamente, en lugar de un punto puede usarse un vector (llamado ''afijo'') que une el origen <math>z=0</math> con el punto P(x,y) del plano. | ||
| + | |||
| + | ===Forma polar de un número complejo=== | ||
| + | Alternativamente, un número complejo puede representarse por su módulo (el del afijo) | ||
| + | |||
| + | <center><math>|z|=\sqrt{x^2+y^2}</math></center> | ||
| + | |||
| + | y su argumento, que es el ángulo que el afijo forma con el eje real | ||
| + | |||
| + | <center><math>\varphi = \mathrm{arctg}\left(\frac{y}{x}\right)</math></center> | ||
| + | ===Conjugado de un número complejo=== | ||
Revisión de 20:05 17 oct 2014
Contenido |
1 Unidad imaginaria
Se define la raíz cuadrada de -1 como la unidad imaginaria
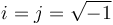
En matemáticas se suele representar como i. En ingeniería como j para evitar confusiones con la intensidad de corriente.
Con ayuda de la unidad imaginaria se puede clacular la raíz de cualquier número negativo
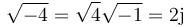
2 Números complejos
Se definen a partir de un par de números reales como
Los números complejos tienen numerosas similitudes con los pares de R2 (x,y) pero con propiedades adicionales.
2.1 Parte real y parte imaginaria
Para un número complejo de la forma anterior
- Parte real
- Es el sumando que no multiplica a la unidad imaginaria
- Parte imaginaria
- Es el coeficiente que multiplica a la unidad imaginaria.
2.2 Representación en el plano complejo
Un número complejo puede representarse como un punto P(x,y) en un plano (denominado plano complejo). La parte real es la abcisa y la imaginaria la ordenada. El eje real es el conjunto de todos los complejos puramente reales y el eje imaginario el de todos los imaginarios puros.
Alternativamente, en lugar de un punto puede usarse un vector (llamado afijo) que une el origen z = 0 con el punto P(x,y) del plano.
2.3 Forma polar de un número complejo
Alternativamente, un número complejo puede representarse por su módulo (el del afijo)
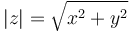
y su argumento, que es el ángulo que el afijo forma con el eje real