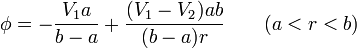Condensador esférico
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
(→Solución) |
||
| Línea 3: | Línea 3: | ||
==Solución== | ==Solución== | ||
| - | En el hueco entre las dos | + | Suponemos la superficie interior a potencial <math>V_0</math> y la exterior a tierra. |
| + | |||
| + | En el hueco entre las dos superficies esféricas no hay carga intermedia, por lo que se verifica la ecuación de Laplace | ||
<center><math>\nabla^2\phi = 0</math></center> | <center><math>\nabla^2\phi = 0</math></center> | ||
| Línea 9: | Línea 11: | ||
con las condiciones de contorno | con las condiciones de contorno | ||
| - | <center><math>\phi = | + | <center><math>\phi = V_0\,</math>{{qquad}}<math>(r=a)\,</math>{{qquad}}{{qquad}}<math>\phi = 0\,</math>{{qquad}}<math>(r=b)\,</math></center> |
Por la simetría del sistema, podemos suponer que el potencial depende exclusivamente de la coordenada radial <math>r</math>. En este caso, la [[Capacidad de una esfera|solución de la ecuación de Laplace]] es de la forma | Por la simetría del sistema, podemos suponer que el potencial depende exclusivamente de la coordenada radial <math>r</math>. En este caso, la [[Capacidad de una esfera|solución de la ecuación de Laplace]] es de la forma | ||
| Línea 17: | Línea 19: | ||
Quedan por determinar las constantes <math>A</math> y <math>B</math>. Sustituyendo las condiciones de contorno | Quedan por determinar las constantes <math>A</math> y <math>B</math>. Sustituyendo las condiciones de contorno | ||
| - | <center><math>A + \frac{B}{a} = | + | <center><math>A + \frac{B}{a} = V_0</math>{{qquad}}<math>A + \frac{B}{b} = 0</math></center> |
resultan las constantes y el potencial | resultan las constantes y el potencial | ||
| - | <center><math>A = \frac{ | + | <center><math>A = -\frac{V_0a}{b-a}</math>{{qquad}}<math>B = \frac{V_0ab}{b-a}</math></center> |
y sustituyendo las constantes en la expresión del potencial | y sustituyendo las constantes en la expresión del potencial | ||
| - | <center><math>\phi = \displaystyle\frac{ | + | <center><math>\phi = \displaystyle-\frac{V_1a}{b-a}+\frac{(V_1-V_2)ab}{(b-a)r}\qquad (a < r < b)</math></center> |
[[Categoría:Problemas de campo eléctrico en presencia de conductores]] | [[Categoría:Problemas de campo eléctrico en presencia de conductores]] | ||
Revisión de 11:48 17 dic 2008
1 Enunciado
Halle la capacidad de un condensador formado por dos superficies esféricas concéntricas, de radios a y b (a < b).
2 Solución
Suponemos la superficie interior a potencial V0 y la exterior a tierra.
En el hueco entre las dos superficies esféricas no hay carga intermedia, por lo que se verifica la ecuación de Laplace

con las condiciones de contorno
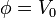

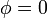
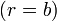
Por la simetría del sistema, podemos suponer que el potencial depende exclusivamente de la coordenada radial r. En este caso, la solución de la ecuación de Laplace es de la forma

Quedan por determinar las constantes A y B. Sustituyendo las condiciones de contorno
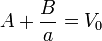
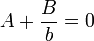
resultan las constantes y el potencial
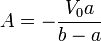
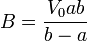
y sustituyendo las constantes en la expresión del potencial