Cuatro conductores paralelos
De Laplace
| Línea 133: | Línea 133: | ||
==Campo y cargas en cada superficie== | ==Campo y cargas en cada superficie== | ||
===Cargas de cada superficie=== | ===Cargas de cada superficie=== | ||
| + | En los cálculos anterios hemos obtenido la carga neta de cada conductor, pero podemos determinar la carga de cada superficie observando que cada una es una placa de un condensador plano. A partir de la diferencia de potencial entre placas podemos hallar estas cargas en todos los casos como | ||
| + | <center><math>Q_{i}=C_{ij}(V_i-V_j)</math></center> | ||
| + | |||
| + | siendo <math>Q_i</math> la carga de la placa i, <math>C_{ij}</math> la capacidad del condensador que ésta forma con la placa j y <math>(V_i-V_j)</math> la diferencia de potencial entre las dos. No obstante, existe más de una forma de hallar estas cargas, muchas veces por simples razonamientos de sumas y restas. | ||
| + | |||
| + | ;Conductor 1: Su placa exterior está descargada. La placa que da al condensador a almacena una carga | ||
| + | |||
| + | <center><math>Q_{1a}=C_a(V_1-V_2)=-50\,\mathrm{nC}</math></center> | ||
| + | |||
| + | :que coincide por supuesto con la total del conductor. | ||
| + | |||
| + | ;Conductor 2: La cara que da al condensador a es opuesta a la que acabamos de hallar | ||
| + | |||
| + | <center><math>Q_{2a}=-Q_{1a}=C_a(V_2-V_1)=+50\,\mathrm{nC}</math></center> | ||
| + | |||
| + | :y la que da al conductor b es el resto de la carga del condensador | ||
| + | |||
| + | <center><math>Q_{2b}=Q_2-Q_{2a}=+50\,\mathrm{nC}</math></center> | ||
| + | |||
| + | ;Conductor 3: La cara que da al condensador b es la opuesta a esta | ||
| + | |||
| + | <center><math>Q_{3b}=-Q_{2b}=-50\,\mathrm{nC}</math></center> | ||
| + | |||
| + | :y puesto que el conductor 3 está descargado, la carga de la otra cara debe anular a ésta | ||
| + | |||
| + | <center><math>Q_{3c}=Q_3-Q_{3b}=0-(-50\,\mathrm{nC})=+50\,\mathrm{nC}</math></center> | ||
| + | |||
| + | ;Conductor 4: Su carga está toda en el condensador c y vale | ||
| + | |||
| + | <center><math>Q_{4c}=-Q_{3c}=-50\,\mathrm{nC}</math></center> | ||
==Estado tras la conexión== | ==Estado tras la conexión== | ||
Revisión de 19:56 16 sep 2014
Contenido |
1 Enunciado
Se tiene un sistema de conductores en forma de bloques prismáticos cuadrados de lado 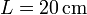 de lado y grosor
de lado y grosor 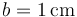 . Estos bloques se sitúan paralelamente de forma que entre el primero y el segundo hay un espacio 3a; entre el 2º y el 3º hay 2a y entre el 3º y el 4º hay a, siendo
. Estos bloques se sitúan paralelamente de forma que entre el primero y el segundo hay un espacio 3a; entre el 2º y el 3º hay 2a y entre el 3º y el 4º hay a, siendo 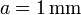 . El espacio entre los conductores está lleno de un dieléctrico ideal de permitividad
. El espacio entre los conductores está lleno de un dieléctrico ideal de permitividad 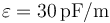 .
.
El conductor 1 y el 4 se encuentran permanentemente a tierra.
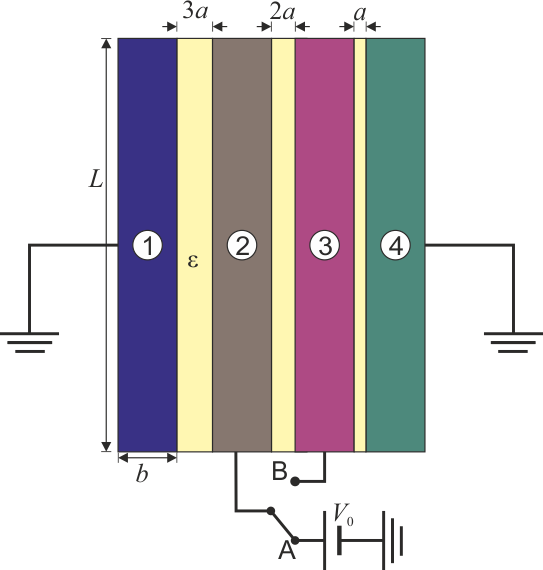
Inicialmente el interruptor se encuentra en la posición A, de forma que el conductor 2 se encuentra a un potencial 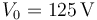 $, mientras que el 3 está aislado y descargado.
$, mientras que el 3 está aislado y descargado.
- Calcule el potencial del conductor 3, así como las cargas netas en cada uno de los cuatro conductores.
- Halle el campo eléctrico en cada uno de los espacios entre conductores, y las cargas almacenadas en cada una de las superficies conductoras
- Suponga que bruscamente se pasa el interruptor de la posición A a la B, conectando los conductores 2 y 3, ¿cómo quedan en ese caso las cargas y potenciales de los diferentes conductores, así como las cargas de cada una de las superficies?
- Halle la energía almacenada en el sistema antes y después de mover el interruptor.
¿Cuánta energía se disipa en el proceso?, ¿cómo puede haber desaparecido esta energía?
2 Potenciales y cargas iniciales
La forma más sencilla de resolver este problema es mediante un circuito equivalente.
Para construir este circuito sustituimos cada conductor por un nodo. Cada par de placas enfrentadas forma un condensador plano, de capacidad
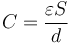
siendo
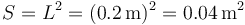
la sección de las placas y d la distancia entre placas, que es distinta en cada caso. Las capacidades de los tres condensadores son
- a. Entre el conductor 1 y el 2
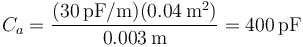
- b. Entre el 2 y el 3
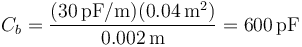
- c. Entre el 3 y el 4
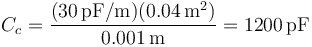
El circuito equivalente al sistema sería entonces el siguiente:
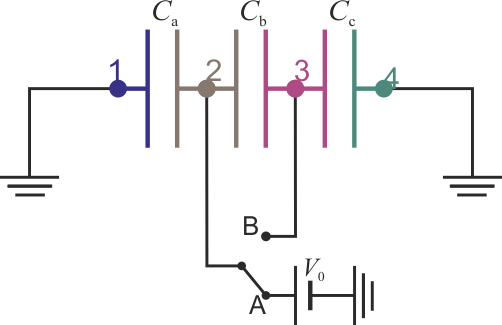
A partir de este circuito podemos construir un sistema de ecuaciones cuya solución nos de las cargas y potenciales que desconocemos, a partir de los datos que sí tenemos
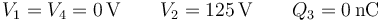
La carga de cada conductor equivale a la suma de las de las placas conectadas al nodo correspondiente. Por tanto
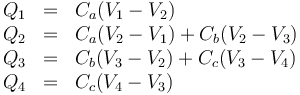
Sustituimos los datos y los valores de las capacidades y queda el sistema (con la carga en nC y el potencial en V)
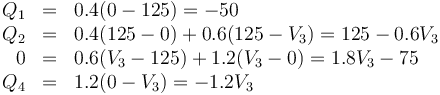
e aquí es inmediato el valor de Q1
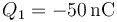
y el de V3
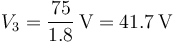
Conocido este dato hallamos Q4
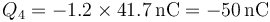
y Q2
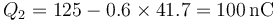
Tabulamos todos los resultados
| Conductor | Q (nC) | V (V) |
|---|---|---|
| 1 | -50 | 0 |
| 2 | 100 | 125 |
| 3 | 0 | 41.7 |
| 4 | -50 | 0 |
Una forma alternativa de llegar a este resultado es reduciendo el circuito equivalente. Sin cambiar las conexiones, podemos dibujarlo como
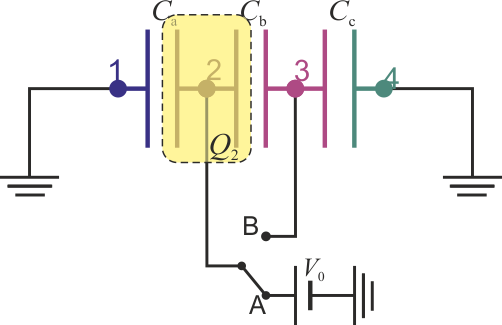
Dado que el conductor 3 está descargado, los condensadores b y c están en serie, cumpliendo su capacidad equivalente
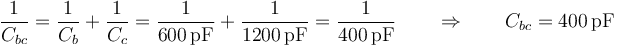
Este condensador está en paralelo con el a, siendo la capacidad equivalente de la asociación completa
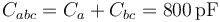
Esto nos da la carga del conductor 2, que corresponde a la placa positiva de este conductor equivalente
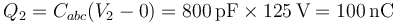
El conductor 1 corresponde a la placa negativa del condensador a, por lo que tiene una carga
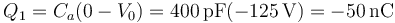
Análogamente, el conductar 4 es la placa negativa del condensador bc
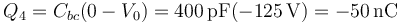
Ya tenemos la carga de los cuatro conductores y el potencial de tres de ellos. Queda hallar el potencial del conductor 3. Éste lo sacamos de que este conductor es la placa positiva del condensador c
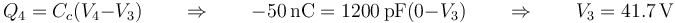
3 Campo y cargas en cada superficie
3.1 Cargas de cada superficie
En los cálculos anterios hemos obtenido la carga neta de cada conductor, pero podemos determinar la carga de cada superficie observando que cada una es una placa de un condensador plano. A partir de la diferencia de potencial entre placas podemos hallar estas cargas en todos los casos como
siendo Qi la carga de la placa i, Cij la capacidad del condensador que ésta forma con la placa j y (Vi − Vj) la diferencia de potencial entre las dos. No obstante, existe más de una forma de hallar estas cargas, muchas veces por simples razonamientos de sumas y restas.
- Conductor 1
- Su placa exterior está descargada. La placa que da al condensador a almacena una carga
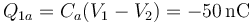
- que coincide por supuesto con la total del conductor.
- Conductor 2
- La cara que da al condensador a es opuesta a la que acabamos de hallar
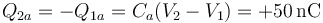
- y la que da al conductor b es el resto de la carga del condensador
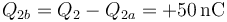
- Conductor 3
- La cara que da al condensador b es la opuesta a esta
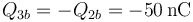
- y puesto que el conductor 3 está descargado, la carga de la otra cara debe anular a ésta
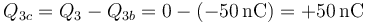
- Conductor 4
- Su carga está toda en el condensador c y vale
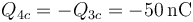
4 Estado tras la conexión
| Conductor | Q (nC) | V (V) |
|---|---|---|
| 1 | -75 | 0 |
| 2 | 75 | 62.5 |
| 3 | 25 | 62.5 |
| 4 | -25 | 0 |
5 Balance energético
- Antes de la conexión
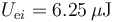
- Después de la conexión
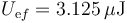
- Energía disipada