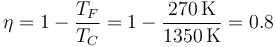Bomba de calor alimentada por máquina térmica
De Laplace
| Línea 22: | Línea 22: | ||
<center>[[Archivo:Esquema-bc-habitacion.png]]</center> | <center>[[Archivo:Esquema-bc-habitacion.png]]</center> | ||
| + | Por tanto, el flujo calor que sale de la máquina térmica debe coincidir con el que escapa de la habitación | ||
| + | |||
| + | <center><math>\dot{Q}_\mathrm{out}=5400\,\mathrm{W}</math></center> | ||
| + | |||
| + | Para obtener la potencia necesaria para hacer funcionar esta máquina aplicamos que el coeficiente de desempeño es | ||
| + | |||
| + | <center><math>\mathrm{COP}_\mathrm{BC}=\frac{\dot{Q}_\mathrm{out}}{\dot{W}_\mathrm{in}}\qquad\Rightarrow\qquad \dot{W}_\mathrm{in}=\frac{\dot{Q}_\mathrm{out}}{\mathrm{COP}_\mathrm{BC}}</math></center> | ||
| + | |||
| + | siendo el de una bomba de calor reversible | ||
| + | |||
| + | <center><math>\mathrm{COP}_\mathrm{BC}^\mathrm{rev}=\frac{T_C}{T_C-T_F}=\frac{300\,\mathrm{K}}{300\,\mathrm{K}-270\,\mathrm{K}}=10</math></center> | ||
| + | |||
| + | por lo que el flujo de trabajo necesario es | ||
| + | |||
| + | <center><math>\dot{W}_\mathrm{in}=\frac{5400\,\mathrm{W}}{10}=540\,\mathrm{W}</math></center> | ||
| + | |||
| + | Esta bomba extrae del foco frío un calor | ||
| + | |||
| + | <center><math>\dot{Q}_\mathrm{in}=\dot{Q}_\mathrm{out}-\dot{W}_\mathrm{in}=4860\,\mathrm{W}</math></center> | ||
==Máquina térmica== | ==Máquina térmica== | ||
| + | Para hacer funcionar la bomba de calor se emplea la máquina térmica. Por tanto, el flujo de trabajo que salga de ésta debe coincidir con el que entra en aquella | ||
| + | |||
| + | <center><math>\dot{W}_\mathrm{out}^\mathrm{MT}=\dot{W}_\mathrm{in}^\mathrm{BC}=540\,\mathrm{W}</math></center> | ||
| + | |||
| + | Este calor se relaciona con el calor absorbido del foco caliente a través del rendimiento | ||
| + | |||
| + | <center><math>\eta=\frac{\dot{W}_\mathrm{out}}{\dot{Q}_\mathrm{in}}\qquad\Rightarrow\qquad \dot{Q}_\mathrm{in}=\frac{\dot{W}_\mathrm{out}}{\eta}</math></center> | ||
| + | |||
| + | siendo éste el de una máquina reversible | ||
| + | |||
| + | <center><math>\eta = 1-\frac{T_F}{T_C}=1-\frac{270\,\mathrm{K}}{1350\,\mathrm{K}}=0.8</math></center> | ||
| + | |||
==Producción de entropía== | ==Producción de entropía== | ||
==Caso no ideal== | ==Caso no ideal== | ||
Revisión de 09:20 24 jun 2014
Contenido |
1 Enunciado
Se desea mantener constante la temperatura de un recinto en 27 °C, siendo la temperatura exterior de −3 °C. El flujo de calor que escapa al exterior es de 5400 W.
- ¿Cuánto vale la resistencia térmica de las paredes?
- Si para mantener la temperatura del recinto se emplea una bomba de calor reversible, ¿cuánto trabajo debe absorber la bomba por segundo?
- Para obtener este trabajo se emplea una máquina térmica, también reversible, que opera entre 1350 K y la temperatura exterior. ¿Cuánto calor toma del foco caliente por segundo y cuánto expulsa al foco frío?
- Para este conjunto de habitación, bomba y máquina, ¿cuánto vale la producción de entropía por segundo en cada uno de los tres elementos y en conjunto?
- Suponga ahora que tanto la bomba de calor como la máquina tienen una eficiencia del 50% respecto a las reversibles. ¿Cuáles son en ese caso las respuestas a las preguntas de los apartados 2, 3 y 4?
2 Resistencia térmica
El flujo de calor a través de un sólido cumple la ley de Fourier
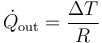
siendo R la resistencia térmica. Despejando
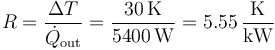
3 Bomba de calor
La bomba de calor se encarga de devolver al interior todo el calor que escapa por la paredes, manteniendo constante la temperatura de la habitación
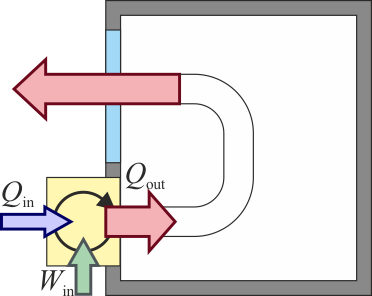
Por tanto, el flujo calor que sale de la máquina térmica debe coincidir con el que escapa de la habitación
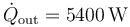
Para obtener la potencia necesaria para hacer funcionar esta máquina aplicamos que el coeficiente de desempeño es
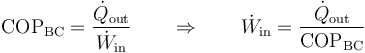
siendo el de una bomba de calor reversible
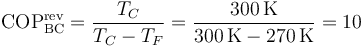
por lo que el flujo de trabajo necesario es
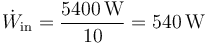
Esta bomba extrae del foco frío un calor
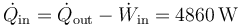
4 Máquina térmica
Para hacer funcionar la bomba de calor se emplea la máquina térmica. Por tanto, el flujo de trabajo que salga de ésta debe coincidir con el que entra en aquella
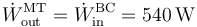
Este calor se relaciona con el calor absorbido del foco caliente a través del rendimiento
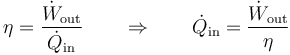
siendo éste el de una máquina reversible