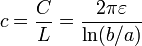Entrar Página Discusión Historial Go to the site toolbox

Condensador coaxial

De Laplace

(Diferencias entre revisiones)
(→Solución)
(→Solución)
Línea 17: Línea 17:
<center><math>\phi(\rho=a) = V_0\,</math>{{qquad}}{{qquad}}<math>\phi(\rho=b) = 0\,</math></center>
<center><math>\phi(\rho=a) = V_0\,</math>{{qquad}}{{qquad}}<math>\phi(\rho=b) = 0\,</math></center>
-
Sin embargo, estas condiciones no son suficientes para resolver el problema. La razón es que la región entre los cilindros no solo está limitada por estos. También hay que incluir los límites en <math>z=0</math> y <math>z=L</math>. Es más, si tenemos en cuenta que el los cilindros son de longitud fihttp://laplace.us.es/wiki/skins/common/images/button_math.pngnita, hay que considerar también las bases de dichos cilindros y la cara exterior del cilindro de fuera, ya que puede haber líneas de campo que vayan desde el interior a esa cara exterior. Si tenemos estos factores en cuenta el problema puede hacerse insoluble numéricamente y requerir solución numérica.
+
Sin embargo, estas condiciones no son suficientes para resolver el problema. La razón es que la región entre los cilindros no solo está limitada por estos. También hay que incluir los límites en <math>z=0</math> y <math>z=L</math>. Es más, si tenemos en cuenta que el los cilindros son de longitud finita, hay que considerar también las bases de dichos cilindros y la cara exterior del cilindro de fuera, ya que puede haber líneas de campo que vayan desde el interior a esa cara exterior. Si tenemos estos factores en cuenta el problema puede hacerse insoluble numéricamente y requerir solución numérica.
El problema se simplifica si se hace la aproximación de despreciar los ''efectos de borde''. Esta aproximación consiste en suponer que los cilindros, aunque de longitud finita, se comportan aproximadamente como si fueran de longitud infinita. Esto se consigue despreciando la contribución de los extremos del cilindro y suponiendo que en todo el espacio entre los cilindros el campo es como en la zona central, donde va radialmente de un cilindro hacia el otro,
El problema se simplifica si se hace la aproximación de despreciar los ''efectos de borde''. Esta aproximación consiste en suponer que los cilindros, aunque de longitud finita, se comportan aproximadamente como si fueran de longitud infinita. Esto se consigue despreciando la contribución de los extremos del cilindro y suponiendo que en todo el espacio entre los cilindros el campo es como en la zona central, donde va radialmente de un cilindro hacia el otro,
Línea 43: Línea 43:
<math><math>\phi=M \ln(\rho)+N</math></math>
<math><math>\phi=M \ln(\rho)+N</math></math>
-
Las constantes <math>M</math> y <math>N</math> se calculan imponiendo las condiciones de
+
Las constantes <math>M</math> y <math>N</math> se calculan imponiendo las condiciones de contorno
-
contorno
+
 
-
\[
+
<center><math>M\ln b+N=0</math>{{qquad}}<math>M\ln a+N=V_0</math></center>
-
M\ln b+N=0\qquad M\ln a+N=V
+
 
-
\]
+
de donde resulta el potencial
de donde resulta el potencial
-
\[
+
 
-
\phi=-V\frac{\ln(\rho/b)}{\ln(b/a)}
+
<center><math>\phi=-V_0\frac{\ln(\rho/b)}{\ln(b/a)}</math></center>
-
\]
+
 
-
El campo lo calculamos como el gradiente del potencial, cambiado de
+
El campo lo calculamos como el gradiente del potencial, cambiado de signo
-
signo
+
 
-
\[
+
<center><math>\mathbf{E}=-\nabla\phi=\frac{V}{\rho\ln(b/a)}\mathbf{u}_{\rho}</math></center>
-
\mathbf{E}=-\nabla\phi=\frac{V}{\rho\ln(b/a)}\mathbf{u}_{\rho}
+
 
-
\]
+
La carga almacenada en la placa interior la hallamos aplicando la ley de Gauss a una superficie cilíndrica, concéntrica con el conductor
-
La carga almacenada en la placa interior la hallamos aplicando la ley
+
interior, de longitud <math>L</math>. Resulta
-
de Gauss a una superficie cilíndrica, concéntrica con el conductor
+
 
-
interior, de longitud $L$. Resulta
+
<center><math>Q=\varepsilon\oint\mathbf{E}{\cdot}\mathrm{d}\mathbf{S}=\varepsilon\int_0^{2\pi}\!\!
-
\[
+
\mathrm{d}\varphi\int_0^L\mathrm{d}z\,\rho\frac{V_0}{\rho\ln(b/a)}=\frac{2\pi\varepsilon L
-
Q=\varepsilon\oint\mathbf{E}{\cdot}\mathrm{d}\mathbf{S}=\varepsilon\int_0^{2\pi}\bs
+
V}{\ln(b/a)}</math></center>
-
d\varphi\int_0^Ldz\rho\frac{V}{\rho\ln(b/a)}=\frac{2\pi\varepsilon L
+
 
-
V}{\ln(b/a)}
+
-
\]
+
De aquí queda, para la capacidad del segmento
De aquí queda, para la capacidad del segmento
-
\[
+
 
-
C=\frac{2\pi\varepsilon L}{\ln(b/a)}
+
<center><math>C=\frac{2\pi\varepsilon L}{\ln(b/a)}</math></center>
-
\]
+
 
y la capacidad por unidad de longitud
y la capacidad por unidad de longitud
-
\[
+
 
-
c=\frac{C}{L}=\frac{2\pi\varepsilon}{\ln(b/a)}
+
<center><math>c=\frac{C}{L}=\frac{2\pi\varepsilon}{\ln(b/a)}</math></center>
-
\]
+
 
[[Categoría:Problemas de campo eléctrico en presencia de conductores]]
[[Categoría:Problemas de campo eléctrico en presencia de conductores]]

Revisión de 20:10 15 dic 2008

1 Enunciado

Un cilindro macizo de gran longitud h y radio a se encuentra rodeado de una corteza cilíndrica concéntrica, la misma longitud L, radio interior b y exterior c, también metálica.

La corteza exterior se encuentra permanentemente a tierra.

Determine la distribución de potencial y de campo eléctrico entre los dos cilindros cuando el cilindro interior se encuentra a potencial V0. Calcule la carga almacenada en el cilindro interior.

Desprecie los efectos de borde.

2 Solución

Para calcular la capacidad de un condensador coaxial debemos resolver el problema del potencial entre las dos superficies cilíndricas. Puesto que no hay carga entre ellas la ecuación es la de Laplace

\nabla^2\phi = 0

con las condiciones de contorno de que el potencial está fijado en ambas superficies cilíndricas

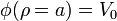
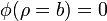
\phi(\rho=a) = V_0\,        \phi(\rho=b) = 0\,

Sin embargo, estas condiciones no son suficientes para resolver el problema. La razón es que la región entre los cilindros no solo está limitada por estos. También hay que incluir los límites en z = 0 y z = L. Es más, si tenemos en cuenta que el los cilindros son de longitud finita, hay que considerar también las bases de dichos cilindros y la cara exterior del cilindro de fuera, ya que puede haber líneas de campo que vayan desde el interior a esa cara exterior. Si tenemos estos factores en cuenta el problema puede hacerse insoluble numéricamente y requerir solución numérica.

El problema se simplifica si se hace la aproximación de despreciar los efectos de borde. Esta aproximación consiste en suponer que los cilindros, aunque de longitud finita, se comportan aproximadamente como si fueran de longitud infinita. Esto se consigue despreciando la contribución de los extremos del cilindro y suponiendo que en todo el espacio entre los cilindros el campo es como en la zona central, donde va radialmente de un cilindro hacia el otro,

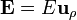
\mathbf{E}= E\mathbf{u}_\rho

Puesto que 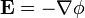\mathbf{E} = -\nabla\phi, igualando la expresión anterior al gradiente en cilíndricas cambiado de signo

\mathbf{E}= E\mathbf{u}_\rho= -\frac{\partial\phi}{\partial\rho}\mathbf{u}_\rho-\frac{1}{\rho}\,\frac{\partial\phi}{\partial\varphi}\mathbf{u}_\varphi-\frac{\partial\phi}{\partial z}\mathbf{u}_z

nos queda

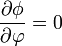
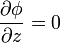
\frac{\partial\phi}{\partial\varphi}=0        \frac{\partial\phi}{\partial z} = 0

Esto equivale, por tanto, a suponer que el potencial eléctrico depende exclusivamente de la coordenada radial ρ.

Otra manera de formularlo consiste en admitir que por la simetría del sistema podemos suponer que el potencial en este hueco no depende de las coordenadas \varphi (lo cual es exactoi) y z (lo cual sólo es aproximado y sólo válido si 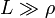L \gg\rho, sino sólo de la coordenada ρ.

Con esta simplificación, la ecuación de Laplace se reduce a

\nabla^2\phi=\frac{1}{\rho}\frac{\mathrm{d}\ }{\mathrm{d}\rho}\left(\rho\frac{\mathrm{d}\phi}{\mathrm{d}\rho}\right)=0

Integrando dos veces, se llega al potencial

< math > φ = Mln(ρ) + N</math>

Las constantes M y N se calculan imponiendo las condiciones de contorno

Mlnb + N = 0    Mlna + N = V0

de donde resulta el potencial

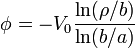
\phi=-V_0\frac{\ln(\rho/b)}{\ln(b/a)}

El campo lo calculamos como el gradiente del potencial, cambiado de signo

\mathbf{E}=-\nabla\phi=\frac{V}{\rho\ln(b/a)}\mathbf{u}_{\rho}

La carga almacenada en la placa interior la hallamos aplicando la ley de Gauss a una superficie cilíndrica, concéntrica con el conductor interior, de longitud L. Resulta

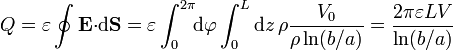
Q=\varepsilon\oint\mathbf{E}{\cdot}\mathrm{d}\mathbf{S}=\varepsilon\int_0^{2\pi}\!\! \mathrm{d}\varphi\int_0^L\mathrm{d}z\,\rho\frac{V_0}{\rho\ln(b/a)}=\frac{2\pi\varepsilon L V}{\ln(b/a)}

De aquí queda, para la capacidad del segmento

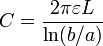
C=\frac{2\pi\varepsilon L}{\ln(b/a)}

y la capacidad por unidad de longitud

c=\frac{C}{L}=\frac{2\pi\varepsilon}{\ln(b/a)}
Obtenido de "http://tesla.us.es/wiki/index.php/Condensador_coaxial"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace