Estática del sólido rígido
De Laplace
(→Teorema de Varignon) |
(→Teorema de Varignon) |
||
| Línea 9: | Línea 9: | ||
La demostración es la siguiente: tenemos <math>n</math> fuerzas concurrentes, <math>\vec{F}_1</math>, <math>\vec{F}_2</math>,... <math>\vec{F}_n</math>, aplicadas en los puntos <math>A_1<math>, <math>A_2</math>,... <math>A_n</math>. El momento resultante respecto a un punto O es | La demostración es la siguiente: tenemos <math>n</math> fuerzas concurrentes, <math>\vec{F}_1</math>, <math>\vec{F}_2</math>,... <math>\vec{F}_n</math>, aplicadas en los puntos <math>A_1<math>, <math>A_2</math>,... <math>A_n</math>. El momento resultante respecto a un punto O es | ||
| - | + | <center><math>\vec{M}_O=\sum_i \overrightarrow{OA}_i\times\vec{F}_i</math></center> | |
Ahora bien, por pasar cada recta soporte por el punto de concurrencia P se cumple para cada una | Ahora bien, por pasar cada recta soporte por el punto de concurrencia P se cumple para cada una | ||
| - | + | <center><math>\overrightarrow{PA}_i\times\vec{F}_i=\vec{0}</math></center> | |
por ser vectores paralelos. Por tanto, para cada momento individual | por ser vectores paralelos. Por tanto, para cada momento individual | ||
| - | + | <center><math>\overrightarrow{OA}_i\times\vec{F}_i = (\overrightarrow{OP}+\overrightarrow{PA}_i)\times\vec{F}_i=\overrightarrow{OP}\times\vec{F}_i</math></center> | |
y para la resultante | y para la resultante | ||
| - | + | <center><math>\vec{M}_O=\sum_i \overrightarrow{OP}\times\vec{F}_i=\overrightarrow{OP}\times\left(\sum_i\vec{F}_i\right)=\overrightarrow{OP}\times\vec{F}</math></center> | |
Por tanto, el procedimiento para hallar el momento resultante consiste en llevar todas las fuerzas al punto de concurrencia, hallar la resultante de todas las fuerzas y luego calcular su momento respecto al punto O. | Por tanto, el procedimiento para hallar el momento resultante consiste en llevar todas las fuerzas al punto de concurrencia, hallar la resultante de todas las fuerzas y luego calcular su momento respecto al punto O. | ||
Revisión de 23:38 2 ene 2014
Contenido |
1 Introducción. Ecuaciones de la estática
2 Teorema de Varignon
De entre los diferentes teoremas aplicables para la determinación de las condiciones de equilibrio, existe uno de especial utilidad, especialmente en el caso de figuras planas, ya que facilita la solución por métodos geométricos.
- Dadas varias fuerzas concurrentes el momento resultante de las distintas fuerzas es igual al momento de la resultante de ellas aplicada en el punto de concurrencia.
Donde entendemos como fuerzas concurrentes aquellas cuyas rectas soporte (que pasan por el punto de aplicación y llevan la dirección de la fuerza) se cortan en un punto O.
La demostración es la siguiente: tenemos n fuerzas concurrentes,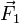 
, 
,... 
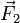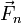, aplicadas en los puntos A1 < math > , < math > A2,... An. El momento resultante respecto a un punto O es
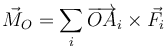
Ahora bien, por pasar cada recta soporte por el punto de concurrencia P se cumple para cada una
por ser vectores paralelos. Por tanto, para cada momento individual
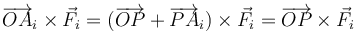
y para la resultante
Por tanto, el procedimiento para hallar el momento resultante consiste en llevar todas las fuerzas al punto de concurrencia, hallar la resultante de todas las fuerzas y luego calcular su momento respecto al punto O.
2.1 Teorema de las tres fuerzas
Un corolario de este teorema es que dado que la resultante de las fuerzas debe anularse, la condición para que un sólido sometido a tres fuerzas esté en equilibrio es que exista un punto P tal que las rectas soporte pasen por él. De esta forma se anulan simultáneamente la resultante de las fuerzas y la de los momentos. Si este punto no existe, el sólido no puede estar en equilibrio.
