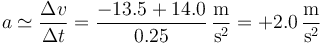Movimiento con datos numéricos
De Laplace
m (→Aceleración instantánea) |
|||
| Línea 98: | Línea 98: | ||
La aceleración la aproximamos como el incremento en la velocidad instantánea dividido por el intervalo de tiempo. El incremento en la velocidad instantánea lo hallamos a partir de la dos valores que acabamos de calcular | La aceleración la aproximamos como el incremento en la velocidad instantánea dividido por el intervalo de tiempo. El incremento en la velocidad instantánea lo hallamos a partir de la dos valores que acabamos de calcular | ||
| - | <center><math>a\simeq \frac{\Delta v}{\Delta t}=\frac{-13.5+14.0}{.25}\,\frac{\mathrm{m}}{\mathrm{s}^2} =+2.0\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center> | + | <center><math>a\simeq \frac{\Delta v}{\Delta t}=\frac{-13.5+14.0}{0.25}\,\frac{\mathrm{m}}{\mathrm{s}^2} =+2.0\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center> |
==Ecuación horaria== | ==Ecuación horaria== | ||
Revisión de 23:05 28 oct 2013
Contenido |
1 Enunciado
La posición de una partícula en distintos instantes de tiempo es, aproximadamente
| t (s) | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 |
|---|---|---|---|---|---|---|---|
| x (m) | 0.000 | 6.125 | 9.750 | 11.250 | 11.000 | 9.375 | 6.750 |
| t (s) | 1.75 | 2.00 | 2.25 | 2.50 | 2.75 | 3.00 |
|---|---|---|---|---|---|---|
| x (m) | 3.500 | 0.000 | -3.375 | -6.250 | -8.250 | -9.000 |
Para este movimiento, halle:
- El desplazamiento entre
y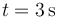 
, así como el valor aproximado de la distancia recorrida en dicho intervalo.
- La velocidad media y la rapidez media en el intervalo anterior.
- El valor aproximado de la velocidad en
.
- El valor aproximado de la aceleración en .
- Sabiendo que este movimiento sigue una ley de la forma
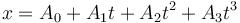
- Calcule
- Los valores de las constantes Ak.
- El valor exacto de la distancia recorrida y la rapidez media.
- El valor exacto de la velocidad y de la aceleración en .
2 Desplazamiento y distancia recorrida
2.1 Desplazamiento
El desplazamiento es simplemente la diferencia entre la posición final y la inicial
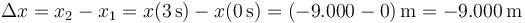
2.2 Distancia
Hallar la distancia total recorrida es un poco más complicado, ya que depende de lo que ocurre durante el movimiento. Tenemos que la partícula parte del origen, se aleja hasta una cierta posición, siendo el máximo aproximado 10.250 m (puede alejarse un poco más en las proximidades de dicho punto y a partir de ahí retrocede de forma continuada hasta la posición final. A la ida recorre esos 11.250 m y a la vuelta los mismos más 9.000 m. La distancia total recorrida será entonces
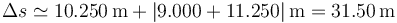
3 Velocidad y rapidez media
3.1 Velocidad media
La velocidad media es el desplazamiento dividido por el intervalo de tiempo empleado en recorrerlo
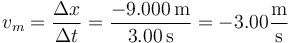
3.2 Rapidez media
Esta es igual a la distancia recorrida dividida por el intervalo de tiempo
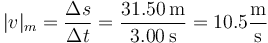
4 Velocidad instantánea
La velocidad instantánea es el límite de la velocidad media cuando el intervalo de tiempo tiende a 0. En este caso no podemos tomar el límite, ya que solo tenemos valores en puntos discretos. Podemos aproximar la velocidad instantánea como la velocidad media entre dos instantes vecinos.
Tomando el intervalo entre 2.00s y 1.75s queda
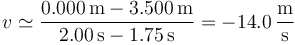
Si tomamos el intervalo entre 2.00s y 2.25s resulta
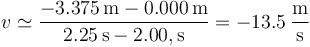
Estos dos valores son próximos pero no iguales. Obtenemos una mejor aproximación tomando la media entre ambos
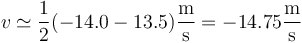
5 Aceleración instantánea
La aceleración la aproximamos como el incremento en la velocidad instantánea dividido por el intervalo de tiempo. El incremento en la velocidad instantánea lo hallamos a partir de la dos valores que acabamos de calcular
