Fuerzas magnéticas (GIE)
De Laplace
(→Fuerza sobre una corriente lineal) |
(→Fuerza sobre una corriente lineal) |
||
| Línea 76: | Línea 76: | ||
<center><math>\vec{B}_0=B_0\vec{k}\qquad\qquad \Delta\vec{r}=l\vec{\jmath}\qquad\Rightarrow\qquad \vec{F}=IlB_0\vec{\jmath}\times\vec{k}=IlB_0\vec{\imath}</math></center> | <center><math>\vec{B}_0=B_0\vec{k}\qquad\qquad \Delta\vec{r}=l\vec{\jmath}\qquad\Rightarrow\qquad \vec{F}=IlB_0\vec{\jmath}\times\vec{k}=IlB_0\vec{\imath}</math></center> | ||
| + | ===De forma arbitraria=== | ||
| + | El cálculo anterior es demasiado simple para una situación general, en la que podemos tener una distribución cualquiera de corriente en un hilo de cualquier forma. Más en general, la fuerza sobre un elemento de corriente es | ||
| + | <center><math>\mathrm{d}\vec{F}=\sum_{q_i\in\Delta v}q_i\vec{v}_i\times \vec{B} = \vec{J}\times\vec{B}\,\mathrm{d}v</math></center> | ||
| - | + | siendo la fuerza total la suma de todos los diferenciales | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<center><math>\vec{F}=\int \vec{J}\times\vec{B}\,\mathrm{d}v</math></center> | <center><math>\vec{F}=\int \vec{J}\times\vec{B}\,\mathrm{d}v</math></center> | ||
| - | |||
| - | |||
Si consideramos un cable, el diferencial de volumen es igual a la sección por la longitud | Si consideramos un cable, el diferencial de volumen es igual a la sección por la longitud | ||
| Línea 101: | Línea 89: | ||
<center><math>\mathrm{d}v=S\,\mathrm{d}l</math></center> | <center><math>\mathrm{d}v=S\,\mathrm{d}l</math></center> | ||
| - | + | y la densidad de corriente se reparte por la sección | |
| + | |||
| + | <center><math>\vec{J}=\frac{I}{S}\vec{u}</math></center> | ||
| + | |||
| + | siendo <math>\vec{u}</math> el unitario a lo largo del hilo. Combinando estos dos factores | ||
<center><math>\vec{F}=\int \frac{I}{S}\vec{u}\times\vec{B}\,S\,\mathrm{d}l=I\int \mathrm{d}\vec{r}\times\vec{B}</math></center> | <center><math>\vec{F}=\int \frac{I}{S}\vec{u}\times\vec{B}\,S\,\mathrm{d}l=I\int \mathrm{d}\vec{r}\times\vec{B}</math></center> | ||
| Línea 107: | Línea 99: | ||
donde podemos sacar la intensidad de la integral, porque es constante a lo largo del cable. También hemos hecho la identificación | donde podemos sacar la intensidad de la integral, porque es constante a lo largo del cable. También hemos hecho la identificación | ||
| - | <center><math>\mathrm{d}\vec{r}\ | + | <center><math>\mathrm{d}\vec{r}=\mathrm{d}l\,\vec{u}</math></center> |
| - | + | ||
| - | + | ||
==Fuerza y par sobre una espira== | ==Fuerza y par sobre una espira== | ||
Revisión de 19:51 13 may 2013
Contenido |
1 Fuerza de Lorentz
1.1 Expresión
Según se ve en el tema de electrostática, la fuerza eléctrica sobre una carga puntual en reposo viene dada por
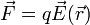
Sin embargo, si dicha carga se encuentra en movimiento, la experiencia muestra que se ve sometida a una fuerza adicional. Esta fuerza, que llamaremos fuerza magnética, verifica que es:
- Proporcional a la carga
- Proporcional al módulo de su velocidad
- Perpendicular a la velocidad
Con estas condiciones, la fuerza magnética debe ser de la forma
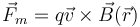
siendo  un nuevo campo, conocido como campo magnético. La fuerza total sobre una carga puntual es entonces
un nuevo campo, conocido como campo magnético. La fuerza total sobre una carga puntual es entonces
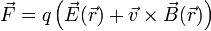
Esta expresión, que es válida en general, tanto para situaciones estáticas como dinámicas, se denomina Fuerza de Lorentz.
1.2 Trabajo magnético nulo
Una propiedad característica de la fuerza magnética sobre una carga magnética es que no realiza trabajo, por siempre normal a la velocidad.
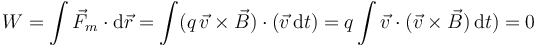
y por tanto permanece constante la energía cinética de una carga que se mueve en un campo magnético.
En términos de las componentes intrínsecas de la aceleración, tenemos que la fuerza es siempre normal a la velocidad y por tanto la aceleración tangencial es siempre nula
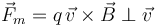

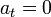
Si la aceleración tangencial es nula, la rapidez (módulo de la velocidad) permanece constante
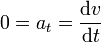

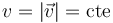
Una rapidez constante implica una energía cinética constante.
Esto quiere decir que una carga puntual que se mueve en el seno de un campo magnético podrá cambiar de dirección de la velocidad (esto es, su movimiento sí será acelerado), pero no se moverá ni más rápido ni más lento en ningún momento.
Hay que destacar que esta conclusión, que el campo magnético no realiza trabajo, es sólo cierta para una carga puntual sometida a la fuerza de Lorentz. Si tenemos una corriente eléctrica (formada por millones de partículas en movimiento) o un dipolo magnético (que también experimenta fuerzas magnéticas) no es cierto que la energía cinética permanezca constante. De hecho, los frenos magnéticos se basan en la disminución de la energía cinética por acción de un campo magnético.
2 Fuerza sobre una corriente lineal
En la naturaleza, raramente se presentan cargas puntuales individualmente. Lo habitual es que formen distribuciones de carga, con miles de millones de ellas en movimientos muy variados. En ese caso, la fuerza magnética sobre una distribución será la resultante de las fuerzas individuales
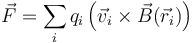
pero, como en otras ocasiones, este sumatorio no es nada útil, pues no conocemos, ni cuantas cargas hay, ni sus posiciones y velocidades. No obstante, podemos emplear esta expresión para deducir a partir de ellas expresiones más prácticas.
Cuando tenemos una corriente eléctrica, existe un movimiento neto de cargas, con una velocidad promedio en la dirección de la corriente. Si ésta se encuentra inmersa en un campo magnético, aparece una fuerza neta sobre la corriente, que sí puede ser medible.
2.1 Rectilínea
Por simplificar el cálculo, supongamos un segmento rectilíneo de longitud l, sección S por el cual circula una intensidad de corriente I y que este segmento se encuentra sumergido en un campo magnético uniforme 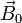 Entonces, en rpomedio, tenemos un flujo de cargas positivas avanzando a lo largo del hilo. Cada una de ellas experimenta una fuerza magnética perpendicular al campo y a la velocidad, es decir, perpendicular a la corriente.
Entonces, en rpomedio, tenemos un flujo de cargas positivas avanzando a lo largo del hilo. Cada una de ellas experimenta una fuerza magnética perpendicular al campo y a la velocidad, es decir, perpendicular a la corriente.
El valor de la fuerza neta será el producto de la cantidad de cargas en movimiento, por la velocidad promedio y por el campo magnético. Si consideramos un solo tipo de portadores, tales que hay N cargas por unidad de volumen, la carga total es
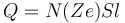
y la fuerza neta
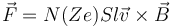
pero
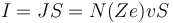
así que podemos expresar esta fuerza como
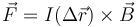
siendo 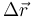 el vector que va del inicio al final del segmento.
el vector que va del inicio al final del segmento.
En el caso particular de que la corriente sea perpendicular al campo, si suponemos que el campo va en la dirección del eje Z, y la velocidad en la del eje Y nos queda
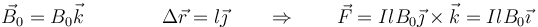
2.2 De forma arbitraria
El cálculo anterior es demasiado simple para una situación general, en la que podemos tener una distribución cualquiera de corriente en un hilo de cualquier forma. Más en general, la fuerza sobre un elemento de corriente es
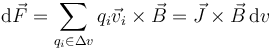
siendo la fuerza total la suma de todos los diferenciales
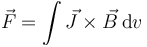
Si consideramos un cable, el diferencial de volumen es igual a la sección por la longitud
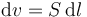
y la densidad de corriente se reparte por la sección
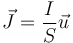
siendo  el unitario a lo largo del hilo. Combinando estos dos factores
el unitario a lo largo del hilo. Combinando estos dos factores
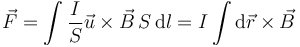
donde podemos sacar la intensidad de la integral, porque es constante a lo largo del cable. También hemos hecho la identificación