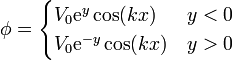Campo y carga de un potencial conocido
De Laplace
(Diferencias entre revisiones)
(→Solución) |
(→Campo eléctrico) |
||
| Línea 11: | Línea 11: | ||
==Solución== | ==Solución== | ||
===Campo eléctrico=== | ===Campo eléctrico=== | ||
| + | Para calcular el campo debemos hallr el gradiente del potencial, cambiado de signo. | ||
| + | |||
| + | <center><math>\mathbf{E}=-\nabla\phi\,</math></center> | ||
| + | |||
| + | Para esto es conveniente separa el potencial en dos regiones | ||
| + | |||
| + | <center><math>\phi = \begin{cases}V_0 \mathrm{e}^y\cos(kx) & y < 0 \\ V_0 \mathrm{e}^{-y}\cos(kx) & y > 0 \end{cases}</math></center> | ||
| + | |||
===Densidad de carga=== | ===Densidad de carga=== | ||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
Revisión de 18:22 18 nov 2008
Contenido |
1 Enunciado
El potencial eléctrico en todos los puntos del espacio viene dado por la ecuación
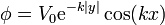
con k y V0 constantes.
- Halle el campo eléctrico en todos los puntos del espacio.
- Calcule la densidad de carga que crea este campo eléctrico.
2 Solución
2.1 Campo eléctrico
Para calcular el campo debemos hallr el gradiente del potencial, cambiado de signo.
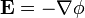
Para esto es conveniente separa el potencial en dos regiones