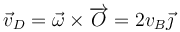Entrar Página Discusión Historial Go to the site toolbox

Diferentes movimientos de una esfera

De Laplace

(Diferencias entre revisiones)
(→Velocidad angular)
(→Método alternativo)
Línea 94: Línea 94:
Puesto que este vector debe ser nulo
Puesto que este vector debe ser nulo
-
<center><math>\omega_y = 0 \qquad\qquad \omega_x+\omega_z\qquad\Rightarrow\qquad \omega_z=-\omega_x</math></center>
+
<center><math>\omega_y = 0 \qquad\qquad \omega_x+\omega_z=0\qquad\Rightarrow\qquad \omega_z=-\omega_x</math></center>
Hallamos ahora la velocidad de B
Hallamos ahora la velocidad de B

Revisión de 20:46 17 ene 2013

Contenido

1 Enunciado

Considérese una esfera de masa M y radio R que se mueve sobre la superficie horizontal z = 0. Consideramos un instante en el que la esfera toca el suelo justo en el origen de coordenadas, O, y tal que en ese momento la velocidad de dicho punto de contacto con el suelo es nula

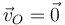
\vec{v}_O = \vec{0}

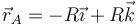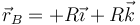Para este mismo instante la velocidad de los puntos \vec{r}_A=-R\vec{\imath}+R\vec{k} y \vec{r}_B=+R\vec{\imath}+R\vec{k} situados en un diámetro horizontal valen respectivamente

\vec{v}_A = v_A\vec{\jmath}\qquad \vec{v}_B = v_B\vec{\jmath}

Para los tres casos siguientes:

(a) vA = + vB
(b) vA = 0
(c) vA = − vB
  1. Indique justificadamente el tipo de movimiento instantáneo que realiza la esfera (traslación, rotación, helicoidal,…)
  2. Calcule la velocidad angular del sólido.
  3. Halle la velocidad angular de pivotamiento y la de rodadura de la esfera.
  4. Dé la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o de rotación, en su caso).
  5. Calcule la velocidad lineal del centro C de la esfera y la del punto D situado en el extremo superior de la esfera.

2 Tipos de movimiento

En los tres casos se cumple lo siguiente:

  • Hay un punto, el de contacto, que tiene velocidad nula
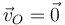
\vec{v}_O=\vec{0}
  • Existe al menos un punto que tiene una velocidad no nula
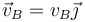
\vec{v}_B = v_B\vec{\jmath}

Por tanto, en los tres casos, el movimiento instantáneo es una rotación alrededor de un eje que pasa por O. (no puede ser uno de reposo, pues hay puntos en movimiento, ni una traslación, por ser diferentes las velocidades, ni helicoidal, por haber alguno con velocidad nula).

Lo que cambiará de un caso a otro s la dirección del eje y el valor de la velocidad angular.

3 Velocidad angular

3.1 Caso (a)

En el primer caso, las velocidades de A y B son iguales

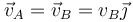
\vec{v}_A=\vec{v}_B=v_B\vec{\jmath}

Esto quiere decir que el eje instantáneo de rotación es paralelo a la recta que pasa por A y B. Dado que

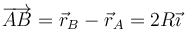
\overrightarrow{AB}=\vec{r}_B-\vec{r}_A =2R\vec{\imath}

la dirección de \vec{\omega} es la de \vec{\imath}

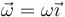
\vec{\omega}=\omega \vec{\imath}

El valor de la cantidad escalar ω lo sacamos de la velocidad de un punto, que puede ser el B

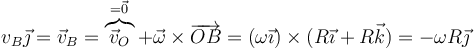
v_B\vec{\jmath}=\vec{v}_B = \overbrace{\vec{v}_O}^{=\vec{0}}+\vec{\omega}\times\overrightarrow{OB} = (\omega\vec{\imath})\times(R\vec{\imath}+R\vec{k})=-\omega R\vec{\jmath}

de donde

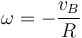
\omega = -\frac{v_B}{R}

A este resultado se puede llegar también geométricamente observando que

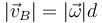
|\vec{v}_B| = |\vec{\omega}| d

siendo d = R la distancia de B al eje instantáneo de rotación (que pasa por O), y toamdno el sentido el dado por la regla de la mano derecha. En forma vectorial, la velocidad angular queda

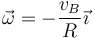
\vec{\omega}=-\frac{v_B}{R}\vec{\imath}

3.2 Caso (b)

En el segundo caso, la velocidad del punto A es nula. Esto nos permite identificar el EIR: es la recta que pasa por los puntos O y A (ambos con velocidad nula). Puesto que la velocidad angular lleva la dirección del eje instantáneo de rotación, debe ser

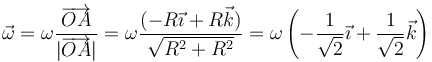
\vec{\omega}=\omega\frac{\overrightarrow{OA}}{|\overrightarrow{OA}|}=\omega \frac{(-R\vec{\imath}+R\vec{k})}{\sqrt{R^2+R^2}}=\omega\left(-\frac{1}{\sqrt{2}}\vec{\imath}+\frac{1}{\sqrt{2}}\vec{k}\right)

Aplicando ahora esta velocidad al cálculo de la velocidad de B

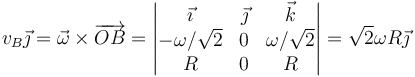
v_B\vec{\jmath}=\vec{\omega}\times\overrightarrow{OB}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -\omega/\sqrt{2} & 0 & \omega/\sqrt{2} \\ R & 0 & R \end{matrix}\right| = \sqrt{2}\omega R\vec{\jmath}

De aquí

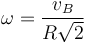
\omega = \frac{v_B}{R\sqrt{2}}

y en forma vectorial

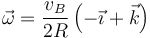
\vec{\omega}=\frac{v_B}{2R}\left(-\vec{\imath}+\vec{k}\right)

3.2.1 Método alternativo

A este mismo resultado se puede llegar sin conocer previamente la dirección de \vec{\omega}. Si suponemos una velocidad angular arbitraria

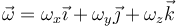
\vec{\omega}=\omega_x\vec{\imath}+\omega_y\vec{\jmath}+\omega_z\vec{k}

y aplicándola al cálculo de la velocidad de A queda

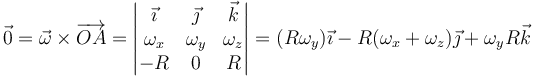
\vec{0}=\vec{\omega}\times\overrightarrow{OA}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \omega_x & \omega_y & \omega_z\\ -R & 0 & R \end{matrix}\right| = (R\omega_y)\vec{\imath}-R(\omega_x+\omega_z)\vec{\jmath}+\omega_yR\vec{k}

Puesto que este vector debe ser nulo

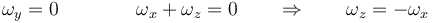
\omega_y = 0 \qquad\qquad \omega_x+\omega_z=0\qquad\Rightarrow\qquad \omega_z=-\omega_x

Hallamos ahora la velocidad de B

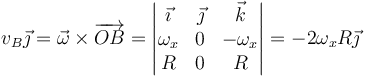
v_B\vec{\jmath}=\vec{\omega}\times\overrightarrow{OB}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \omega_x & 0 & -\omega_x \\ R & 0 & R \end{matrix}\right| = -2\omega_x R\vec{\jmath}

De aquí

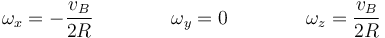
\omega_x = -\frac{v_B}{2R}\qquad\qquad \omega_y = 0\qquad\qquad \omega_z = \frac{v_B}{2R}

y en forma vectorial

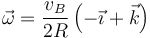
\vec{\omega}=\frac{v_B}{2R}\left(-\vec{\imath}+\vec{k}\right)

como habíamos dicho.

3.3 Caso (c)

En el tercer caso, las velocidades de los puntos A y B son opuestas.

Como en el caso anterior, podemos suponer una velocidad angular genérica

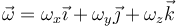
\vec{\omega}=\omega_x\vec{\imath}+\omega_y\vec{\jmath}+\omega_z\vec{k}

y la aplicamos al cálculo de las velocidades de A y B. Para el punto A

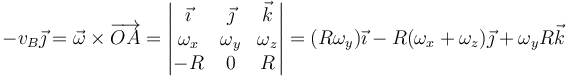
-v_B\vec{\jmath}=\vec{\omega}\times\overrightarrow{OA}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \omega_x & \omega_y & \omega_z\\ -R & 0 & R \end{matrix}\right| = (R\omega_y)\vec{\imath}-R(\omega_x+\omega_z)\vec{\jmath}+\omega_yR\vec{k}

Igualando componente a componente

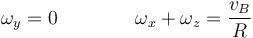
\omega_y=0\qquad\qquad \omega_x+\omega_z=\frac{v_B}{R}

Para el punto B

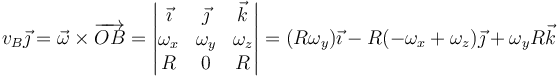
v_B\vec{\jmath}=\vec{\omega}\times\overrightarrow{OB}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \omega_x & \omega_y & \omega_z\\ R & 0 & R \end{matrix}\right| = (R\omega_y)\vec{\imath}-R(-\omega_x+\omega_z)\vec{\jmath}+\omega_yR\vec{k}

que nos da ahora

\omega_y=0\qquad\qquad -\omega_x+\omega_z=\frac{v_B}{R}

De estas ecuaciones y las anteriores nos queda

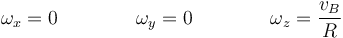
\omega_x = 0\qquad\qquad \omega_y=0\qquad\qquad \omega_z=\frac{v_B}{R}

y en forma vectorial

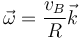
\vec{\omega}=\frac{v_B}{R}\vec{k}

Este resultado también se podía haber previsto por razonamientos geométricos. Dada la simetría de las velocidades, es fácil ver que la esfera está girando alrededor de un eje vertical que pasa por el punto de apoyo (es decir, está pivotando). Al estar los puntos A y B en lados opuestos del eje y a la misma distancia de éste, resultan velocidades del mismo módulo y dirección, pero de sentido opuesto.

4 Pivotamiento y rodadura

4.1 Caso (a)

Puesto que en el primer caso la velocidad es puramente tangencial a la superficie, el movimiento que describe la esfera es de rodadura, sin deslizamiento ni pivotamiento, siendo

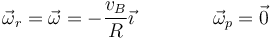
\vec{\omega}_r = \vec{\omega}=-\frac{v_B}{R}\vec{\imath}\qquad \qquad \vec{\omega}_p=\vec{0}

5 Eje instantáneo de rotación

Según hemos dicho, en los tres casos, el movimiento instantáneo es de rotación. No tenemos entonces un EIRMD, sino simplemente un EIR. Además sabemos que la velocidad del punto de contacto, O, es nula, por lo que el EIR pasa por él. Queda simplemente escribir su dirección, que la da la velocidad angular.

5.1 Caso (a)

En el primer caso, la velocidad horizontal es tangente al plano, según la dirección del vector \vec{\imath}. Por tanto, el eje es simplemente

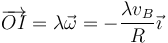
\overrightarrow{OI}=\lambda\vec{\omega}=-\frac{\lambda v_B}{R}\vec{\imath}

o, puesto que la definición de λ es arbitraria, podemos escribirlo más sencillamente

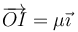
\overrightarrow{OI}=\mu\vec{\imath}

Es decir, el EIR coincide con el eje OX.

5.2 Caso (b)

5.3 Caso (c)

6 Velocidad de dos puntos

6.1 Caso (a)

Una vez que tenemos la velocidad de un punto y la velocidad angular podemos hallar la velocidad instantánea de cualquier otro.

El centro de la esfera se encuentra en la posición, respecto al origen O

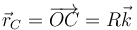
\vec{r}_C = \overrightarrow{OC}=R\vec{k}

siendo su velocidad lineal instantánea

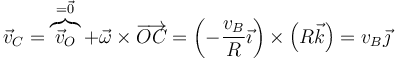
\vec{v}_C = \overbrace{\vec{v}_O}^{=\vec{0}} + \vec{\omega}\times\overrightarrow{OC}=\left(-\frac{v_B}{R}\vec{\imath}\right)\times\left(R\vec{k}\right)=v_B\vec{\jmath}

Resulta una velocidad igual a la de los puntos A y B, ya que el centro de la esfera se encuentra sobre la recta que pasa por estos dos puntos.

Para el punto D

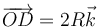
\overrightarrow{OD}=2R\vec{k}

y resulta una velocidad que es el doble de la del punto C

\vec{v}_D=\vec{\omega}\times\overrightarrow{O}=2v_B\vec{\jmath}

6.2 Caso (b)

6.3 Caso (c)

Obtenido de "http://tesla.us.es/wiki/index.php/Diferentes_movimientos_de_una_esfera"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace