Base ortonormal dextrógira
De Laplace
(→...y que cumplen la regla de la mano derecha) |
(→...ortogonales,...) |
||
| Línea 14: | Línea 14: | ||
\mathbf{u}_2\cdot\mathbf{u}_3 = 0</math></center> | \mathbf{u}_2\cdot\mathbf{u}_3 = 0</math></center> | ||
| - | La condición de ortonormalidad (carácter unitario más ortogonalidad) se puede expresar de forma compacta con ayuda de la Delta de Kronecker | + | La condición de ortonormalidad (carácter unitario más ortogonalidad) se puede expresar de forma compacta con ayuda de la ''Delta de Kronecker'' |
<center><math>\mathbf{u}_i\cdot\mathbf{u}_k = \delta_{ik} = \left\{\begin{array}{ll}1 & i=k \\ 0 & i\neq k\end{array}\right.</math></center> | <center><math>\mathbf{u}_i\cdot\mathbf{u}_k = \delta_{ik} = \left\{\begin{array}{ll}1 & i=k \\ 0 & i\neq k\end{array}\right.</math></center> | ||
| + | |||
| + | o, en forma matricial, | ||
| + | |||
| + | <center><math>\left(\delta_{ik}\right)=\pmatrix{1 & 0 & 0\cr 0 & 1 & 0 \cr 0 & 0 1}</math></center> | ||
==...y que cumplen la regla de la mano derecha== | ==...y que cumplen la regla de la mano derecha== | ||
Revisión de 18:22 21 nov 2007
Contenido |
1 Definición
Una base vectorial se dice que es ortonormal dextrógira, si sus vectores son unitarios, ortogonales, y verifican la regla de la mano derecha.
2 Vectores unitarios,...
Un vector es unitario cuando su módulo es la unidad. Matemáticamente, esto quiere decir que si la base vectorial es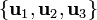 
se cumple
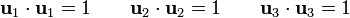
3 ...ortogonales,...
Una base es ortonormal cuando además de ser unitaria, sus vectores son ortogonales entre sí. Esto se expresa como
La condición de ortonormalidad (carácter unitario más ortogonalidad) se puede expresar de forma compacta con ayuda de la Delta de Kronecker
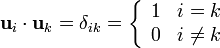
o, en forma matricial,
4 ...y que cumplen la regla de la mano derecha
Se dice que un conjunto ordenado de tres vectores ortonormales cumple la regla de la mano derecha (o, técnicamente, es dextrógiro) cuando el producto vectorial de los dos primeros da el tercero:
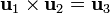
y como consecuencia de lo anterior
y también
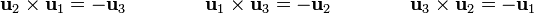
La forma compacta de escribir esta fórmula es mediante el símbolo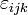 
, que verifica
