Masa de esfera no homogénea
De Laplace
| Línea 1: | Línea 1: | ||
| + | __TOC__ | ||
==Enunciado== | ==Enunciado== | ||
| - | + | Se tiene una distribución de masa con simetría esférica, con una densidad | |
| + | dependiente de la posición tal que | ||
| - | <center><math>\rho = A(R-r)\ | + | <center><math>\rho(\vec{r})=\begin{cases}A(R-r) & r < R \\ 0 & r > R\end{cases}</math></center> |
| - | + | siendo <math>r = |\vec{r}|</math> la distancia al centro de la esfera. Halle la masa total de la esfera. | |
| - | == | + | ==Solución== |
| - | + | Puesto que la densidad depende de la posición, no podemos hallar la masa total simplemente multiplicando densidad por volumen. Cuando la densidad es función de la posición, lo más que podemos asegurar es que si consideremos un elemento de volumen de tamaño diferencial, la masa de este elemento es | |
| - | + | <center><math>\mathrm{d}m = \rho(\vec{r})\,\mathrm{d}V</math></center> | |
| - | + | de forma que la masa total del sistema es la suma de las masas de cada uno de los elementos en que se divide | |
| - | + | <center><math>M = \int_M \mathrm{d}m = \int_V \rho(\vec{r})\,\mathrm{d}V</math></center> | |
| - | |||
| - | + | [[Archivo:capas-cebolla-02.png|300px|left]] | |
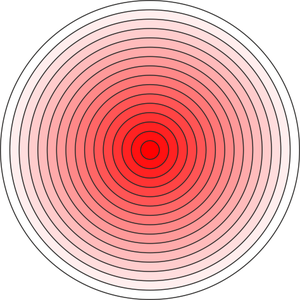
| - | < | + | Por ser la densidad uniforme para cada valor de <math>r</math>, lo más sencillo es tomar como elementos de volumen capas esféricas de espesor diferencial, como las de una cebolla. Cada una de estas capas, de radio <math>r</math> (comprendido entre <math>0</math> y <math>R</math>), es una lámina de área <math>4\pi r^2</math> y espesor <math>\mathrm{d}r</math>, por lo que tiene un volumen diferencial |
| - | == | + | <center><math>\mathrm{d}V = Sh = 4\pi r^2\,\mathrm{d}r</math></center> |
| - | + | ||
| - | + | ||
| - | + | La masa de cada una de estas capas será igual a la densidad de masa multiplicada por el volumen | |
| - | + | ||
| - | + | ||
<center><math>\mathrm{d}m = \rho\,\mathrm{d}V = 4\pi A(R-r)r^2\,\mathrm{d}r</math></center> | <center><math>\mathrm{d}m = \rho\,\mathrm{d}V = 4\pi A(R-r)r^2\,\mathrm{d}r</math></center> | ||
| - | Dado que la densidad varía al aumentar el radio <math>r</math>, el centro de la esfera es la parte más densa | + | Dado que la densidad varía al aumentar el radio <math>r</math>, el centro de la esfera es la parte más densa. Llevando esto a la integral |
| - | Llevando esto a la integral | + | |
<center><math>M = 4\pi A\int_0^R (R-r)r^2\,\mathrm{d}r = 4\pi A\left(R\int_0^R r^2\,\mathrm{d}r-\int_0^R r^3\,\mathrm{d}r\right)=4\pi A\left(R\frac{R^3}{3}-\frac{R^4}{4}\right)=\frac{\pi A R^4}{3}</math></center> | <center><math>M = 4\pi A\int_0^R (R-r)r^2\,\mathrm{d}r = 4\pi A\left(R\int_0^R r^2\,\mathrm{d}r-\int_0^R r^3\,\mathrm{d}r\right)=4\pi A\left(R\frac{R^3}{3}-\frac{R^4}{4}\right)=\frac{\pi A R^4}{3}</math></center> | ||
Una comprobación que siempre conviene hacer es verificar que las dimensiones son correctas y que a la hora de descomponer en dos integrales, no nos hemos olvidado ninguna potencia de <math>R</math>. | Una comprobación que siempre conviene hacer es verificar que las dimensiones son correctas y que a la hora de descomponer en dos integrales, no nos hemos olvidado ninguna potencia de <math>R</math>. | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
[[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | [[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | ||
última version al 18:27 15 dic 2012
Contenido |
1 Enunciado
Se tiene una distribución de masa con simetría esférica, con una densidad dependiente de la posición tal que
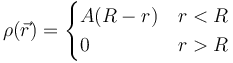
siendo  la distancia al centro de la esfera. Halle la masa total de la esfera.
la distancia al centro de la esfera. Halle la masa total de la esfera.
2 Solución
Puesto que la densidad depende de la posición, no podemos hallar la masa total simplemente multiplicando densidad por volumen. Cuando la densidad es función de la posición, lo más que podemos asegurar es que si consideremos un elemento de volumen de tamaño diferencial, la masa de este elemento es
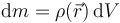
de forma que la masa total del sistema es la suma de las masas de cada uno de los elementos en que se divide
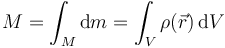
Por ser la densidad uniforme para cada valor de r, lo más sencillo es tomar como elementos de volumen capas esféricas de espesor diferencial, como las de una cebolla. Cada una de estas capas, de radio r (comprendido entre 0 y R), es una lámina de área 4πr2 y espesor dr, por lo que tiene un volumen diferencial
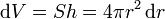
La masa de cada una de estas capas será igual a la densidad de masa multiplicada por el volumen
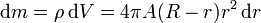
Dado que la densidad varía al aumentar el radio r, el centro de la esfera es la parte más densa. Llevando esto a la integral
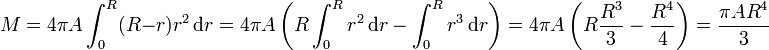
Una comprobación que siempre conviene hacer es verificar que las dimensiones son correctas y que a la hora de descomponer en dos integrales, no nos hemos olvidado ninguna potencia de R.