Potencial en el centro de una esfera
De Laplace
(→Por integración directa) |
(→Por integración directa) |
||
| Línea 13: | Línea 13: | ||
La expresión integral para el potencial eléctrico debido a una distribución superficial de carga es | La expresión integral para el potencial eléctrico debido a una distribución superficial de carga es | ||
| - | <center><math>\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\int_S \frac{\sigma_s(\mathbf{r | + | <center><math>\phi(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\int_S \frac{\sigma_s(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\,\mathrm{d}S'</math></center> |
| - | En nuestro caso la superficie de integración es la esfera de radio R, en cuyo centro situamos el origen de coordenadas, que es la posición en que queremos hallar el potencial. Por ello | + | En nuestro caso la superficie de integración es la esfera de radio <math>R</math>, en cuyo centro situamos el origen de coordenadas, que es la posición en que queremos hallar el potencial. Por ello |
| - | <center><math>\mathbf{r} = \mathbf{0}</math>{{qquad}}<math>\mathbf{r'} = R\mathbf{u}_{r'}</math>{{qquad}} <math>|\mathbf{r}-\mathbf{r}'|=R</math> | + | <center><math>\sigma_s = \sigma_0 = \frac{Q}{4\pi R^2}</math>{{qquad}}<math>\mathbf{r} = \mathbf{0}</math>{{qquad}}<math>\mathbf{r'} = R\mathbf{u}_{r'}</math>{{qquad}} <math>|\mathbf{r}-\mathbf{r}'|=R</math></math></center> |
| + | |||
| + | Sustituyendo todo esto nos queda | ||
| + | |||
| + | <center><math>\phi(\mathbf{0}) = \frac{1}{4\pi\varepsilon_0}\,\frac{Q}{4\pi R^2}\int_S \frac{\mathrm{d}S'}{R} = \frac{Q}{4\pi\varepsilon_0 R}</math></center> | ||
| + | |||
| + | El resultado es un potencial análogo al que crearía una carga puntual situada a una distancia <math>R</math>. La razón es evidente: el centro de la esfera se encuentra a la misma distancia de todos los puntos de la superficie. Por tanto la contribución de cada elemento de superficie al potencial es simplemente la carga en dicho elemento dividida por la distancia, que es siempre la misma, y la constante <math>1/4\pi\varepsilon_0</math>. El resultado es la carga total dividida por <math>1/4\pi\varepsilon_0</math> y por <math>R</math>. | ||
====A partir del campo eléctrico==== | ====A partir del campo eléctrico==== | ||
Revisión de 20:13 6 nov 2008
Contenido |
1 Enunciado
Calcule el potencial eléctrico en el centro de una esfera de radio R, cargada con una carga Q0 distribuida…
- uniformemente en su superficie
- de forma no uniforme en su superficie, con densidad σs = σ0cosθ.
- uniformemente en su volumen
- en su volumen con una densidad ρ = Ar (calcule previamente el valor de la constante A).
2 Solución
2.1 Esfera cargada uniformemente en la superficie
En este caso de una carga en el centro de una esfera, la simetría del problema permite hacer el cálculo de forma sencilla tanto por integración directa como a partir del campo eléctrico.
2.1.1 Por integración directa
La expresión integral para el potencial eléctrico debido a una distribución superficial de carga es
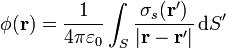
En nuestro caso la superficie de integración es la esfera de radio R, en cuyo centro situamos el origen de coordenadas, que es la posición en que queremos hallar el potencial. Por ello
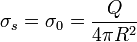
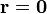
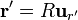
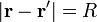</math>Sustituyendo todo esto nos queda
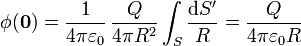
El resultado es un potencial análogo al que crearía una carga puntual situada a una distancia R. La razón es evidente: el centro de la esfera se encuentra a la misma distancia de todos los puntos de la superficie. Por tanto la contribución de cada elemento de superficie al potencial es simplemente la carga en dicho elemento dividida por la distancia, que es siempre la misma, y la constante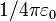 
. El resultado es la carga total dividida por 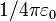y por R.
