Escalas y gráficas logarítmicas
De Laplace
(→Introducción. Comportamientos no lineales) |
(→Reducción a una forma lineal) |
||
| Línea 10: | Línea 10: | ||
===Reducción a una forma lineal=== | ===Reducción a una forma lineal=== | ||
A modo de ejemplo, si tenemos el problema de de una partícula que cae desde una cierta altura, y medimos el tiempo de caída, podemos obtener una tabla como la siguiente | A modo de ejemplo, si tenemos el problema de de una partícula que cae desde una cierta altura, y medimos el tiempo de caída, podemos obtener una tabla como la siguiente | ||
| + | |||
| + | [[Archivo:hfrenteat.png|500px|right]] | ||
{| class="bordeado" | {| class="bordeado" | ||
| Línea 40: | Línea 42: | ||
Por ello la gráfica teórica de h frente al tiempo es una parábola. Si representamos la altura frente al tiempo, obtenemos una serie de puntos no alineados | Por ello la gráfica teórica de h frente al tiempo es una parábola. Si representamos la altura frente al tiempo, obtenemos una serie de puntos no alineados | ||
| - | |||
| - | |||
Aunque podemos ajustar una recta de mínimos cuadrados, esto no sirve absolutamente de nada, porque ni los puntos están alineados, ni la pendiente de esa recta tiene significado físico. | Aunque podemos ajustar una recta de mínimos cuadrados, esto no sirve absolutamente de nada, porque ni los puntos están alineados, ni la pendiente de esa recta tiene significado físico. | ||
En cambio, si representamos h frente al cuadrado del tiempo, añadiendo una nueva columna | En cambio, si representamos h frente al cuadrado del tiempo, añadiendo una nueva columna | ||
| + | |||
| + | [[Archivo:hfrenteat2.png|500px|right]] | ||
{| class="bordeado" | {| class="bordeado" | ||
| Línea 84: | Línea 86: | ||
La gráfica en este caso si es aproximadamente recta, y de su pendiente podemos hallar el valor de la aceleración de la gravedad | La gráfica en este caso si es aproximadamente recta, y de su pendiente podemos hallar el valor de la aceleración de la gravedad | ||
| - | |||
B = | B = | ||
Revisión de 16:28 22 nov 2012
Contenido |
1 Introducción. Comportamientos no lineales
En la mayoría de las prácticas de física, las leyes que se han de verificar siguen una dependencia lineal
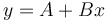
Sin embargo, no hay que pensar que ésta es la forma general de una dependencia entre funciones. Las magnitudes se relacionarán en general por fórmulas des lo más variopintas (exponenciales, polinomios, logaritmos, funciones trigonométricas) y en muchos casos ni siquiera existe una fórmula conocida que permita relacionar dos magnitudes.
La ventaja de las rectas de mejor ajuste es que son las más sencillas. Disponemos de fórmulas para la pendiente, la ordenada en el origen y sus respectivas incertidumbres, y podemos representarlas fácilmente. Por ello, siempre que sea posible, es preferible reducir el problema a una dependencia lineal.
1.1 Reducción a una forma lineal
A modo de ejemplo, si tenemos el problema de de una partícula que cae desde una cierta altura, y medimos el tiempo de caída, podemos obtener una tabla como la siguiente
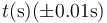
| 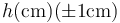
|
|---|---|
| 0.54 | 140 |
| 0.50 | 120 |
| 0.45 | 100 |
| 0.41 | 80 |
| 0.36 | 60 |
| 0.28 | 40 |
La teoría nos dice que el tiempo que tarda en caer cumple
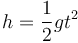
Por ello la gráfica teórica de h frente al tiempo es una parábola. Si representamos la altura frente al tiempo, obtenemos una serie de puntos no alineados
Aunque podemos ajustar una recta de mínimos cuadrados, esto no sirve absolutamente de nada, porque ni los puntos están alineados, ni la pendiente de esa recta tiene significado físico.
En cambio, si representamos h frente al cuadrado del tiempo, añadiendo una nueva columna
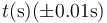
| t2(s2) | 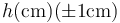
|
|---|---|---|
| 0.54 | 0.292(6) | 140 |
| 0.50 | 0.250(5) | 120 |
| 0.45 | 0.202(4) | 100 |
| 0.41 | 0.168(3) | 80 |
| 0.36 | 0.130(3) | 60 |
| 0.28 | 0.078(15) | 40 |
(nótese que ahora cada dato tiene un error diferente), la nueva dependiencia teórica es lineal, ya que
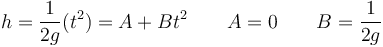
La gráfica en este caso si es aproximadamente recta, y de su pendiente podemos hallar el valor de la aceleración de la gravedad
B =
1.2 Dependencia exponencial
Supongamos que la relación funcional supuesta es de la forma
En este caso, tomando logaritmos en los dos miembros queda
que podemos reescribir como
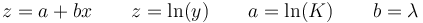
esto es, que si a partir de las salidas yi hallamos sus respectivos logaritmos, zi y calculamos la recta de mejor ajuste de zi frente a los xi, el resultado es una recta que nos da los parámetros K y λ. El factor del exponente coincide con la pendiente de la recta, mientras que el prefactor K vale
Los errores de λ y A serán
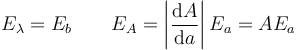
Para obtener gráficamente una recta en este caso deberemos representar ln(y) frente a x.
1.3 Dependencia potencial
En ocasiones debemos suponer que entre la entrada y la salida existe una relación potencial de la forma
y el objetivo es determinar el exponente α y el prefactor k. Esto lo conseguimos hallando el logaritmo de cada miembro
que se puede escribir como
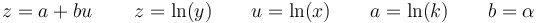
es decir, que si se representa gráficamente ln(y) frente a ln(x) (lo que se denomina una gráfica log-log) deberemos obtener un comportamiento aproximadamente lineal.
Los errores del prefactor y del exponente serán

2 Escalas logarítmicas
Cuando se tienen datos de los que se sabe, o se sospecha, que poseen una conducta exponencial o potencial, interesa usar como eje el logaritmo de una o de las dos cantidades. Sin embargo, al indicar en los ejes dichos logaritmos, las gráficas son más difíciles de interpretar. Es mucho más fácil entender una gráfica en la que los puntos corresponden a “2” y a “3”' que una en que corresponden a “0.301” y “0.477” (los logaritmos decimales de 2 y 3).
Nos interesa entonces una representación que, aun estando las marcas espaciadas según los logaritmos de 1, 2, 3,…, las etiquetas corresponden a “1”, “2”, “3”,… de forma que sabemos a qué valor original corresponde cada logaritmo.
Para construir esta escala logarítmica se emplea usualmente la base 10. Se sitúa la marca de “1” en el origen (pues su logaritmo es 0) y “10” a una distancia unitaria (por ejemplo, 1 cm). Los valores correspondientes a “2”, “3”, etc., se situarán a 0.301 cm, 0.477 cm, etc. del origen.
Esto produce una escala no lineal, en la que las marcas se van acumulando. Así, la distancia entre 100 y 10 es la misma que entre 10 y 1, y la marca del 20 dista del 10, lo mismo que la del 2 de la del 1.

El uso de estas escalas es especialmente útil cuando se tienen un rango de datos muy amplio, como por ejemplo, al hacer un barrido en frecuencias. Empleando una escala logarítmica se le da la misma importancia a las bajas frecuencias que a las altas. Por ejemplo, para la respuesta un circuito RLC, la representación en una escala logarítmica muestra la simetría del comportamiento para altas y bajas frecuencias:
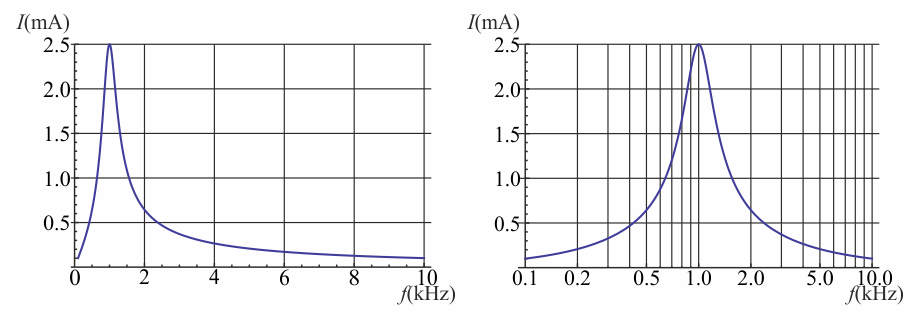
3 Gráficas con escalas logarítmicas
Combinando los diferentes tipos de escalas, podemos tener gráficas semilogarítmicas, cuando una de las dos escalas es logarítmica y la otra lineal (útil para comportamientos exponenciales y logarítmicos), y logarítmicas (o log-log), cuando las dos escalas son logarítmicas (apropiado para comportamientos potenciales).
No es necesario diseñar manualmente este tipo de escalas: los programas de representación gráfica, como Excel, permiten seleccionar escalas logarítmicas. También existen papeles milimetrados con una o dos escalas logarítmicas.
Por ejemplo, supongamos que tenemos los datos
| r (cm) | V (V) |
|---|---|
| 2 | 9.93 |
| 3 | 7.44 |
| 4 | 5.54 |
| 5 | 4.11 |
| 6 | 3.18 |
| 7 | 2.02 |
| 8 | 1.25 |
| 9 | 0.85 |
| 10 | 0.02 |
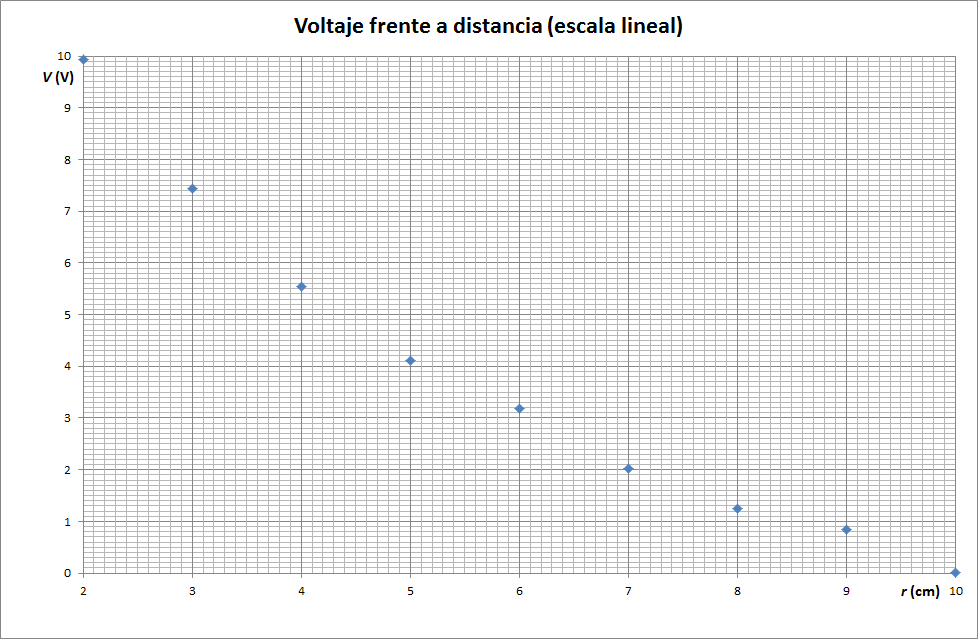
Si representamos el voltaje respecto a la distancia, obtenemos una gráfica como la de la figura. En esta apreciamos un decrecimiento con r pero que no es totalmente lineal. Esa curvatura podría obedecer a una exponencial, una parábola, un logaritmo,…
Si la tabla anterior la representamos en una gráfica semilogarítmica, en la que una de las dos escalas (la de la distancia) es logarítmica, mientras que la del voltaje es lineal, el resultado es claramente rectilíneo, por lo que debemos suponer una dependencia de la forma V = a + bln(r)
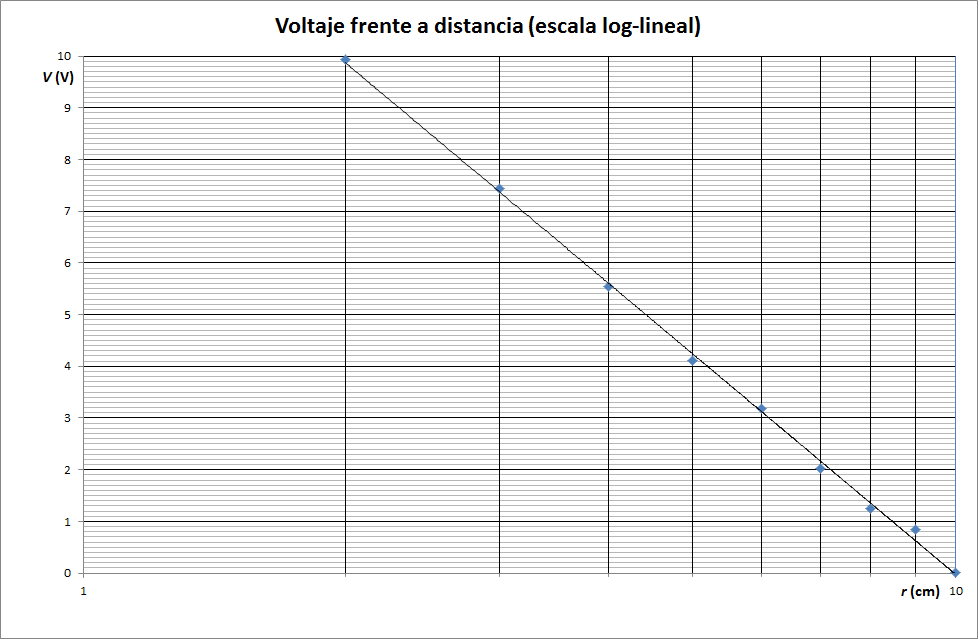
Como otro ejemplo, supongamos la siguiente tabla de datos
| x (cm) | B (mT) |
|---|---|
| 0.5 | 24.83 |
| 1.0 | 12.79 |
| 1.5 | 8.45 |
| 2.0 | 6.58 |
| 2.5 | 4.90 |
| 3.0 | 4.02 |
| 3.5 | 3.37 |
| 4.0 | 2.96 |
| 4.5 | 2.57 |
| 5.0 | 2.57 |
| 5.5 | 2.34 |
| 6.0 | 2.36 |
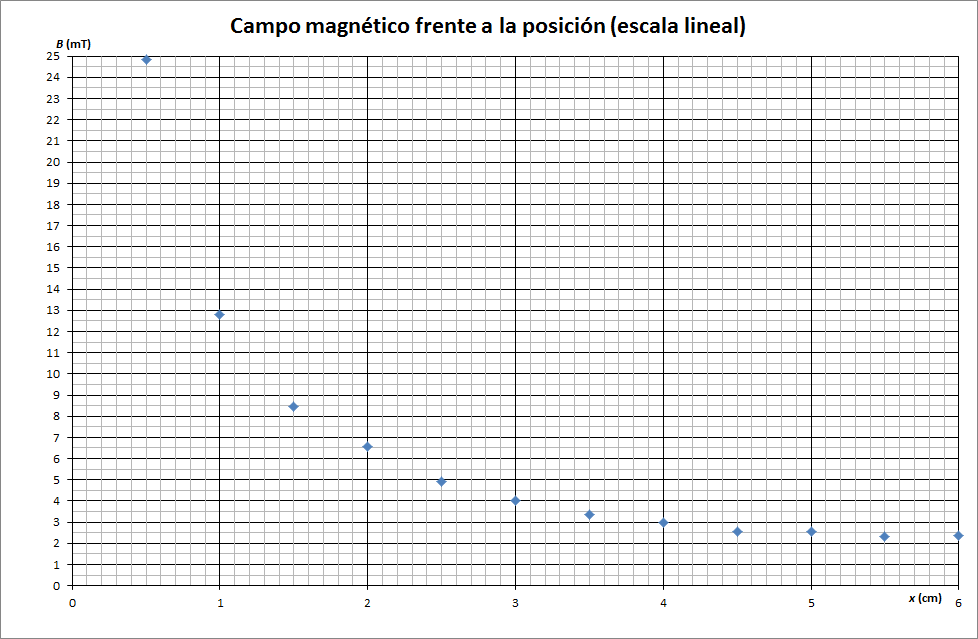
En una representación con escalas lineales, la gráfica podría ser un decaimiento exponencial, o una hipérbola, u otros comportamientos.
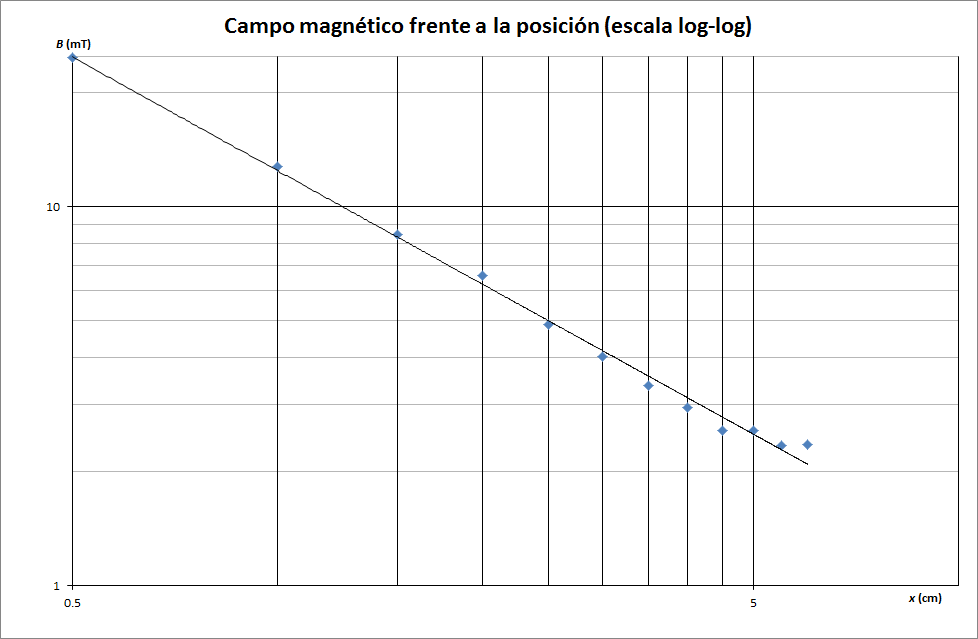
Si hacemos la representación en una gráfica log-log, vemos la ley teórica es una potencial, pues en esta gráfica muestra un comportamiento lineal. Es más, midiendo la pendiente en esta representación resulta un valor próximo a -1, lo que indica que sigue una ley B = K / x.







