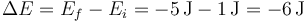3.10. Energía potencial lineal a tramos (Ex.Dic/11)
De Laplace
(→Energía mecánica) |
(→Puntos de retorno) |
||
| Línea 17: | Línea 17: | ||
Los puntos de retorno son aquellos en los que la celeridad de la partícula se anula instantáneamente y se invierte el sentido del movimiento de la misma. Corresponden a los valores de <math>x\,</math> para los cuales se produce intersección entre la gráfica de energía potencial y la recta horizontal representativa de la energía mecánica constante e igual a 1 J. Observamos que existen dos puntos de retorno: | Los puntos de retorno son aquellos en los que la celeridad de la partícula se anula instantáneamente y se invierte el sentido del movimiento de la misma. Corresponden a los valores de <math>x\,</math> para los cuales se produce intersección entre la gráfica de energía potencial y la recta horizontal representativa de la energía mecánica constante e igual a 1 J. Observamos que existen dos puntos de retorno: | ||
<center><math> | <center><math> | ||
| - | x_1=-4\,\mathrm{m}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x_2=5\,\mathrm{m} | + | x_1=-4\,\mathrm{m}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\, x_2=5\,\mathrm{m} |
</math></center> | </math></center> | ||
Dado que se nos indica que en el instante inicial la partícula se halla en <math>x=4\,\mathrm{m}</math> moviéndose en el sentido positivo del eje OX, es obvio que primero se alcanzará el punto de retorno que hemos llamado <math>x_2\,</math>, y posteriormente el llamado <math>x_1\,</math>. | Dado que se nos indica que en el instante inicial la partícula se halla en <math>x=4\,\mathrm{m}</math> moviéndose en el sentido positivo del eje OX, es obvio que primero se alcanzará el punto de retorno que hemos llamado <math>x_2\,</math>, y posteriormente el llamado <math>x_1\,</math>. | ||
Revisión de 01:42 13 oct 2012
Contenido |
1 Enunciado
Una partícula de masa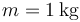 
se mueve a lo largo del eje OX, sometida a la acción de una fuerza conservativa cuya energía potencial es la de la gráfica. En el instante inicial se encuentra en 
moviéndose en el sentido positivo del eje OX con celeridad 
.
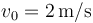- Halle la energía mecánica de la partícula.
- Se detiene en algún punto, ¿en cuál? Una vez que retorna, ¿dónde se vuelve a detener?
- Halle la fuerza sobre la partícula, así como su aceleración, en los dos puntos de retorno.
- ¿Qué tipo de movimiento describe la partícula entre cada punto de retorno y
?
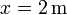- Suponga que la masa se ve sometida adicionalmente a una fuerza de rozamiento que la va frenando hasta detenerla por completo. ¿Dónde se detiene finalmente? ¿Cuánta energía mecánica se ha disipado desde el instante inicial hasta el instante en que la partícula se detiene definitivamente?
2 Energía mecánica
Se trata de un movimiento rectilíneo conservativo. La energía mecánica (suma de la cinética y la potencial) es constante en el tiempo. La calculamos evaluándola en el instante inicial:
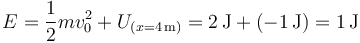
3 Puntos de retorno
Los puntos de retorno son aquellos en los que la celeridad de la partícula se anula instantáneamente y se invierte el sentido del movimiento de la misma. Corresponden a los valores de 
para los cuales se produce intersección entre la gráfica de energía potencial y la recta horizontal representativa de la energía mecánica constante e igual a 1 J. Observamos que existen dos puntos de retorno:
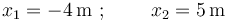
Dado que se nos indica que en el instante inicial la partícula se halla en moviéndose en el sentido positivo del eje OX, es obvio que primero se alcanzará el punto de retorno que hemos llamado 
, y posteriormente el llamado 
.
4 Fuerza y aceleración en los puntos de retorno
En el caso unidimensional que nos ocupa, la fuerza que soporta la partícula en cada posición coincide con la pendiente de la energía potencial cambiada de signo. Por tanto:
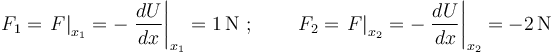
Pero en realidad hemos llamado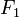 
(y 
) a la componente-x de la fuerza (la única componente que existe en este problema unidimensional). Así que, vectorialmente:
Y la aceleración se obtiene dividiendo la fuerza por la masa (1 kg), conforme a la segunda ley de Newton:
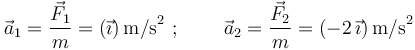
5 Tipo de movimiento
Entre cada punto de retorno y el punto 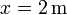, la gráfica de energía potencial es una recta (pendiente constante). Por tanto, en cada uno de esos dos tramos la fuerza es constante, la aceleración también, y el movimiento es rectilíneo y uniformemente acelerado.
6 Caso con rozamiento: punto en que se detiene y energía disipada
En caso de que exista una fuerza de rozamiento, la energía mecánica de la partícula va disminuyendo por conversión en energía calorífica. En tal caso, la representación gráfica de la energía mecánica deja de ser una recta horizontal. El descenso paulatino del nivel de energía mecánica da lugar a que los puntos de retorno (intersección de energía mecánica y energía potencial) se vayan acercando entre sí cada vez más. Y al final la partícula se detendrá definitivamente (se quedará sin energía cinética de forma permanente) en la posición correspondiente al mínimo de energía potencial (
), es decir, en .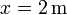
Y la energía mecánica disipada desde el instante inicial hasta el instante en que la partícula se ha detenido definitivamente habrá sido:
