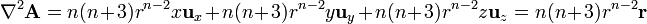Cálculo de laplaciano vectorial

De Laplace

(Diferencias entre revisiones)

Revisión de 12:37 3 oct 2008

Contenido

1 Enunciado
2 Solución
- 2.1 Empleando la identidad vectorial
- 2.2 Empleando la base cartesiana

1 Enunciado

Halle el laplaciano del campo vectorial

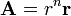
$\mathbf{A}=r^n\mathbf{r}\,$

2 Solución

Una posibilidad, a la hora de resolver este problema, consiste en expresar este vector en la base cartesiana, y hallar el laplaciano de cada componente, ya que

$\nabla^2\mathbf{A} = \left(\nabla^2A_x\right)\mathbf{u}_x+\left(\nabla^2A_y\right)\mathbf{u}_y+\left(\nabla^2A_z\right)\mathbf{u}_z$

Sin embargo, este método exige largos y engorrosos cálculos (ya que esta fórmula no es válida en componentes esféricas, en las que el campo se escribe de forma sencilla), por lo que en su lugar es preferible emplear la identidad vectorial

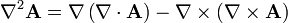
$\nabla^2\mathbf{A}=\nabla\left(\nabla\cdot\mathbf{A}\right)-\nabla\times\left(\nabla\times\mathbf{A}\right)$

que requiere el cálculo de gradientes, divergencias y rotacionales, lo que podemos hacer en diferentes sistemas de coordenadas.

Veremos, de todas formas, ambos métodos.

2.1 Empleando la identidad vectorial

2.2 Empleando la base cartesiana

Si expresamos el vector $\mathbf{A}$ tanto en sus componentes como en sus coordenadas cartesianas queda

$\mathbf{A}=(x^2+y^2+z^2)^{n/2}\left(x\mathbf{u}_x+y\mathbf{u}_y+z\mathbf{u}_z\right)$

Las componentes del laplaciano de este vector son iguales a los laplacianos de las componentes

$\left(\nabla^2\mathbf{A}\right)_x = \nabla^2A_x = \nabla^2\left((x^2+y^2+z^2)^{n/2}x\right)$

El cálculo directo es largo (y además proclive a los errores), por lo que es preferible emplear la regla de la cadena escribiendo la operación como

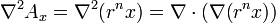
$\nabla^2A_x = \nabla^2(r^nx) = \nabla\cdot(\nabla(r^n x))$

Aplicando ahora el gradiente de un producto tenemos

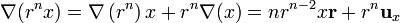
$\nabla(r^n x) = \nabla\left(r^n\right)x+r^n\nabla(x) = nr^{n-2}x\mathbf{r}+r^n\mathbf{u}_x$

ya que

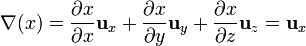
$\nabla(r^n) = n r^{n-2}\mathbf{r}$ $\nabla(x) = \frac{\partial x}{\partial x}\mathbf{u}_x+\frac{\partial x}{\partial y}\mathbf{u}_y+\frac{\partial x}{\partial z}\mathbf{u}_z = \mathbf{u}_x$

Calculamos la divergencia de cada sumando por separado. Para el primero

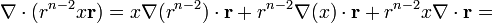
$\nabla\cdot(r^{n-2}x\mathbf{r}) = x\nabla(r^{n-2})\cdot\mathbf{r}+ r^{n-2}\nabla(x)\cdot\mathbf{r}+r^{n-2}x\nabla\cdot\mathbf{r}=$

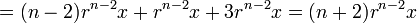
$=(n-2)r^{n-2}x+r^{n-2}x+3r^{n-2}x = (n+2)r^{n-2}x\,$

y para el segundo

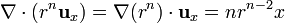
$\nabla\cdot\left(r^n\mathbf{u}_x\right) = \nabla(r^n)\cdot\mathbf{u}_x = nr^{n-2}x$

Sumando las dos contribuciones

$\nabla(r^n x)=n(n+2)r^{n-2}x+nr^{n-2}x=n(n+3)r^{n-2}x$

y el laplaciano vectorial es

$\nabla^2\mathbf{A} = n(n+3)r^{n-2}x\mathbf{u}_x+n(n+3)r^{n-2}y\mathbf{u}_y+n(n+3)r^{n-2}z\mathbf{u}_z = n(n+3)r^{n-2}\mathbf{r}$

@@ Línea 58: / Línea 58: @@
 y el laplaciano vectorial es
-<center><math>\nabla^2\mathbf{A} = n(n+3)r^{n-2}x\mathbf{u}_x+n(n+3)r^{n-2}y\mathbf{u}_y+n(n+3)r^{n-2}z\mathbf{u}_z = n{n+3}r^{n-2}\mathbf{r}</math></center>
+<center><math>\nabla^2\mathbf{A} = n(n+3)r^{n-2}x\mathbf{u}_x+n(n+3)r^{n-2}y\mathbf{u}_y+n(n+3)r^{n-2}z\mathbf{u}_z = n(n+3)r^{n-2}\mathbf{r}</math></center>
 [[Categoría:Problemas de fundamentos matemáticos]]

Cálculo de laplaciano vectorial

De Laplace

Revisión de 12:37 3 oct 2008

Contenido

1 Enunciado

2 Solución

2.1 Empleando la identidad vectorial

2.2 Empleando la base cartesiana

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES