Enfriado de agua con hielo GIA
De Laplace
(→Hipótesis A) |
(→Hipótesis A) |
||
| Línea 14: | Línea 14: | ||
Dado que la cantidad de agua es cuatro veces la hielo y que la diferencia de temperatura de aquélla (<math>T_\mathrm{a}</math>) con respecto a la del punto de congelación (<math>T_0</math>), es cinco veces mayor que la de éste respecto de la del hielo (<math>T_\mathrm{h}</math>), resulta una hipótesis plausible que la temperatura de equilibrio, <math>T</math>, esté por encima de la del punto de congelación. | Dado que la cantidad de agua es cuatro veces la hielo y que la diferencia de temperatura de aquélla (<math>T_\mathrm{a}</math>) con respecto a la del punto de congelación (<math>T_0</math>), es cinco veces mayor que la de éste respecto de la del hielo (<math>T_\mathrm{h}</math>), resulta una hipótesis plausible que la temperatura de equilibrio, <math>T</math>, esté por encima de la del punto de congelación. | ||
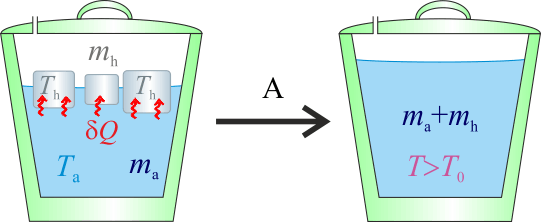
| - | [[Archivo:bol_T2_04_1.gif|right]]Nótese que esta hipótesis, implica que toda la masa de hielo debe haberse fundido, mientras que la de agua sólo habrá reducido su temperatura. Es decir, el resultado final de la mezcla tras el proceso serían <math>1250\,\mathrm{g}\,</math> de agua a una temperatura <math>\displaystyle{}\, T > T_0</math>. | + | [[Archivo:bol_T2_04_1.gif|right]]Nótese que esta hipótesis, implica que toda la masa de hielo debe haberse fundido, mientras que la de agua sólo habrá reducido su temperatura. Es decir, el resultado final de la mezcla tras el proceso serían <math>1250\,\mathrm{g}\,</math> de agua a una temperatura\, <math>\displaystyle{}\, T > T_0</math>. |
Revisión de 13:44 12 jun 2012
1 Enunciado
Para enfriar un litro de agua que está a 20°C se le añaden 250 gramos de hielo a -4°C. Determinar el estado final de la mezcla supuestas despreciables las pérdidas de calor.
Datos: calor específico del hielo, 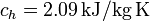 ; calor latente de fusión del hielo,
; calor latente de fusión del hielo, 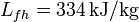 .
.
2 Solución
En primer lugar, consideraremos que la mezcla inicial de hielo y agua se encuentra en un recipiente de paredes fijas, a una presión aproximada de una atmósfera y que, según se indica en el enunciado, las cantidad de calor que intercambia aquél con la mezcla son despreciables. En consecuencia, las únicas transferencias de energía a tener en cuenta, serán las que existan entre la masas 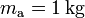 de agua, y
de agua, y 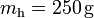 de hielo. Por otra parte, como la primera sustancia es un líquido incompresible, y el hielo es un sólido, admitiremos que la única forma posible de transferencia de energía será en forma de calor, debido a las diferentes temperaturas que inicialmente tienen los componentes de la mezcla. Obsérvese que, como éstos son la misma sustancia pero en diferente fase, las cantidades de calor transferidas en el proceso que termina en el equilibrio térmico, van a producir tanto cambios de temperatura, como cambios de fase, que determinarán el estado final de la mezcla que, a su vez estará condicionado por la temperatura final de equilibrio.
de hielo. Por otra parte, como la primera sustancia es un líquido incompresible, y el hielo es un sólido, admitiremos que la única forma posible de transferencia de energía será en forma de calor, debido a las diferentes temperaturas que inicialmente tienen los componentes de la mezcla. Obsérvese que, como éstos son la misma sustancia pero en diferente fase, las cantidades de calor transferidas en el proceso que termina en el equilibrio térmico, van a producir tanto cambios de temperatura, como cambios de fase, que determinarán el estado final de la mezcla que, a su vez estará condicionado por la temperatura final de equilibrio.
A priori, no podemos asegurar cuál va a ser dicho estado final, y no tenenos más remedio que establecer ciertas hipótesis de trabajo y comprobar si el resultado que se obtiene, es compatible con aquéllas.
2.1 Hipótesis A
Dado que la cantidad de agua es cuatro veces la hielo y que la diferencia de temperatura de aquélla (Ta) con respecto a la del punto de congelación (T0), es cinco veces mayor que la de éste respecto de la del hielo (Th), resulta una hipótesis plausible que la temperatura de equilibrio, T, esté por encima de la del punto de congelación.
Nótese que esta hipótesis, implica que toda la masa de hielo debe haberse fundido, mientras que la de agua sólo habrá reducido su temperatura. Es decir, el resultado final de la mezcla tras el proceso serían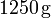 de agua a una temperatura\,
de agua a una temperatura\, 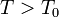 .
.