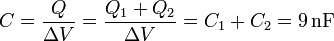Sistema de dos condensadores en paralelo (F2GIA)
De Laplace
(→Solución) |
(→Solución) |
||
| Línea 8: | Línea 8: | ||
==Solución== | ==Solución== | ||
| - | Al estar asociados en paralelo, cada conductor de un condensador será equipotencial con uno de los conductores del otro. De esta forma, al conectar el sistema a una batería, en ambos condensadores existirá idéntica diferencia de potencial <math>\Delta V</math>. En consecuencia, cada condensador adquirirá la carga correspondiente a su capacidad. Si la diferencia de potencial provocada por la batería es de <math> | + | Al estar asociados en paralelo, cada conductor de un condensador será equipotencial con uno de los conductores del otro. De esta forma, al conectar el sistema a una batería, en ambos condensadores existirá idéntica diferencia de potencial <math>\Delta V</math>. En consecuencia, cada condensador adquirirá la carga correspondiente a su capacidad. Si la diferencia de potencial provocada por la batería es de <math>6\,\mathrm{V}\,</math>, dichas cargas serán: |
| - | <center><math>Q_1=C_1\!\ \Delta V= | + | <center><math>Q_1=C_1\!\ \Delta V= 36\,\mathrm{nC}\ \mathrm{;}\,\quad Q_2=C_2\!\ \Delta V= 18\,\mathrm{nC} |
</math></center> | </math></center> | ||
| + | |||
| + | Al desconectar la batería, estas cargas permanecen en los conductores, de manera que también se mantendrá la diferencia de potencial <math>\Delta V=6\,\mathrm{V}\,</math>. Por otra parte, la capacidad de la asociación será igual a la relación entre la carga total que hay en el conductor resultante de conectar las placas de los dos condensadores, y la diferencia de potencial existente: | ||
| + | |||
| + | <center><math>C=\frac{Q}{\Delta V}=\frac{Q_1+Q_2}{\Delta V}=C_1+C_2=9\,\mathrm{nF}\,</math></center> | ||
Revisión de 17:18 20 abr 2012
1 Enunciado
Dos condensadores planos, ambos de la misma sección y con aire entre los planos, tienen capacidades eléctricas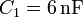 
y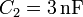 
. Los condensadores están conectados formando una asociación en paralelo, que se mantendrá en todo momento. La asociación descrita se conecta a una batería adquiriendo los condensadores una diferencia de potencial 
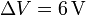. Después, se desconecta la asociación de la batería y se rellena todo el espacio existente entre las placas del segundo condensador (C2) con un material de constante dieléctrica κ desconocida, y que soporta un campo eléctrico de 
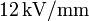antes de la ruptura dieléctrica.
- ¿Cuál debe ser el valor de κ para que la nueva diferencia de potencial en los condensadores de la asociación sea
?
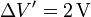- Teniendo en cuenta que el aire sólo soporta un campo de
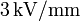, calcular la relación entre la energía máxima que puede almacenar la asociación en paralelo de los dos condensadores en la situación final (cuando el segundo condensador está relleno del dieléctrico), y la energía máxima correspondiente a la situación inicial de los condensadores con aire.
2 Solución
Al estar asociados en paralelo, cada conductor de un condensador será equipotencial con uno de los conductores del otro. De esta forma, al conectar el sistema a una batería, en ambos condensadores existirá idéntica diferencia de potencial ΔV. En consecuencia, cada condensador adquirirá la carga correspondiente a su capacidad. Si la diferencia de potencial provocada por la batería es de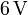 
, dichas cargas serán:
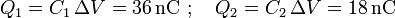
Al desconectar la batería, estas cargas permanecen en los conductores, de manera que también se mantendrá la diferencia de potencial 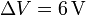. Por otra parte, la capacidad de la asociación será igual a la relación entre la carga total que hay en el conductor resultante de conectar las placas de los dos condensadores, y la diferencia de potencial existente:
