Capacidad de un condensador cilíndrico GIA
De Laplace
(→Solución) |
(→Solución) |
||
| Línea 9: | Línea 9: | ||
El condensador cilíndrico o coaxial está formado por dos superficies conductoras cilíndricas coaxiales <math>\mathrm{C}_1</math> y <math>\mathrm{C}_2</math>, de radios <math>R_1</math> y <math>R_2</math>, respectivamente, separadas por un medio no conductor. Ambas tienen igual longitud <math>L</math>, que deberá ser significativamente mayor que los radios de las superficies para poder considerar que las cargas eléctricas se distribuyen uniformemente en ellas. Además, para poder asegurar que se encuentran en influencia total o próximos a ella (requisito para que formen un condensador), es conveniente que la distancia de separación entre las placas sea suficientemente menor que el radio de la superficie interior; es decir, <math>R_2-R_1\ll R_1</math>. | El condensador cilíndrico o coaxial está formado por dos superficies conductoras cilíndricas coaxiales <math>\mathrm{C}_1</math> y <math>\mathrm{C}_2</math>, de radios <math>R_1</math> y <math>R_2</math>, respectivamente, separadas por un medio no conductor. Ambas tienen igual longitud <math>L</math>, que deberá ser significativamente mayor que los radios de las superficies para poder considerar que las cargas eléctricas se distribuyen uniformemente en ellas. Además, para poder asegurar que se encuentran en influencia total o próximos a ella (requisito para que formen un condensador), es conveniente que la distancia de separación entre las placas sea suficientemente menor que el radio de la superficie interior; es decir, <math>R_2-R_1\ll R_1</math>. | ||
| + | ===Distribuciones de carga y campo eléctrico=== | ||
Si se cumplen las condiciones geométricas expresadas anteriormente, cuando las placas se encuentran cargadas y a diferente potencial, todas las líneas de campo eléctrico que salen de la superficie <math>\mathrm{C}_1</math> terminan en la <math>\mathrm{C}_2</math>. Esto se traduce en que ambas superficies van a almacenar cantidades opuestas de carga eléctrica. Además, la verificación simultánea de las condiciones geométricas | Si se cumplen las condiciones geométricas expresadas anteriormente, cuando las placas se encuentran cargadas y a diferente potencial, todas las líneas de campo eléctrico que salen de la superficie <math>\mathrm{C}_1</math> terminan en la <math>\mathrm{C}_2</math>. Esto se traduce en que ambas superficies van a almacenar cantidades opuestas de carga eléctrica. Además, la verificación simultánea de las condiciones geométricas | ||
Revisión de 13:05 24 mar 2012
1 Enunciado
Calcular la capacidad de un condensador cilíndrico de radio interior R1, radio exterior R2 y longitud L suponiendo que 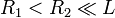 .
.
Si se sumerge parcialmente en líquido dieléctrico lineal, ¿cuál es su nueva capacidad? ¿Cómo cambia la energía acumulada en el condensador?
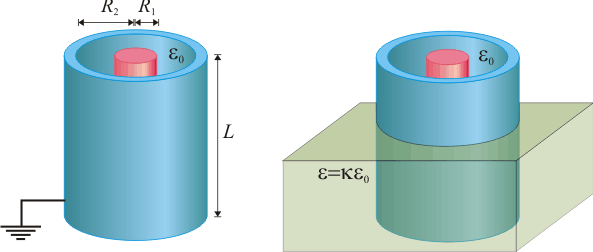
2 Solución
El condensador cilíndrico o coaxial está formado por dos superficies conductoras cilíndricas coaxiales C1 y C2, de radios R1 y R2, respectivamente, separadas por un medio no conductor. Ambas tienen igual longitud L, que deberá ser significativamente mayor que los radios de las superficies para poder considerar que las cargas eléctricas se distribuyen uniformemente en ellas. Además, para poder asegurar que se encuentran en influencia total o próximos a ella (requisito para que formen un condensador), es conveniente que la distancia de separación entre las placas sea suficientemente menor que el radio de la superficie interior; es decir, 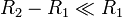 .
.
2.1 Distribuciones de carga y campo eléctrico
Si se cumplen las condiciones geométricas expresadas anteriormente, cuando las placas se encuentran cargadas y a diferente potencial, todas las líneas de campo eléctrico que salen de la superficie C1 terminan en la C2. Esto se traduce en que ambas superficies van a almacenar cantidades opuestas de carga eléctrica. Además, la verificación simultánea de las condiciones geométricas
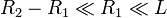
nos permite realizar una serie de simplificaciones sobre cómo van a distribuirse las cargas en las superficies conductoras y cómo es el campo eléctrico en el sistema, sin que estas aproximaciones afecten significativamente al resultado que obtendremos para la capacidad eléctrica. Así, consideraremos que una cantidad Q de carga en el conductor interior C1 se distribuirá uniformemente en la superficie de este se distribuirá uniformemente en la superfie enfrentada al C2. Y por estar en influencia total, en la correspondiente superficie de este conductor existirá una cantidad opuesta de carga, también distribuida uniformemente. Es decir, en las superficie enfrentadas de C1 y C2 existen sendas densidades superficiales de carga, constantes:
despreciándose las acumulaciones de carga en los bordes de dichas superficies (efectos de borde). Observese que si el conductor C2 es una “corteza” esférica, existirá otra superficie cilíndrica conductora exterior,  de radio mayor que R2, en la que también podría almacenarse carga eléctrica (por ejemplo, en caso de que este conductor estuviese inicialmente descargado y aislado). Sin embargo, el condensador cilíndrico objeto de estudio es el constituido, únicamente, por la superficie
de radio mayor que R2, en la que también podría almacenarse carga eléctrica (por ejemplo, en caso de que este conductor estuviese inicialmente descargado y aislado). Sin embargo, el condensador cilíndrico objeto de estudio es el constituido, únicamente, por la superficie  (de radio R1) y la interior
(de radio R1) y la interior  (de radio R2) del conductor C2.
(de radio R2) del conductor C2.





