Esfera conductora hueca con carga puntual GIA

De Laplace

Revisión de 17:54 16 mar 2012 (ver código fuente) Gabriel (Discusión | contribuciones) (→Solución) ← Edición más antigua		Revisión de 17:54 16 mar 2012 (ver código fuente) Gabriel (Discusión | contribuciones) (→Solución) Edición más nueva →
Línea 5:		Línea 5:
	==Solución==		==Solución==
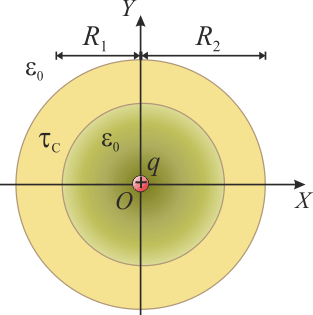
-	En la figura se muestra una sección transversal del sistema bajo estudio. Se trata de una esfera conductora de radio <math>R_2</math>, en cuyo interior hay un hueco esférico y concéntrico de radio <math>R_1</math>, que se encuentra vacío salvo en su centro <math>O</math>, donde hay situada una carga puntual de valor <math>q</math>.	+	En la figura se muestra una sección transversal del sistema bajo estudio. Se trata de una esfera conductora de radio <math>R_2</math>, descargada y aislada, en cuyo interior hay un hueco esférico y concéntrico de radio <math>R_1</math>, que se encuentra vacío salvo en su centro <math>O</math>, donde hay situada una carga puntual de valor <math>q</math>.

---

Revisión de 17:54 16 mar 2012

1 Enunciado

Una esfera conductora hueca de radios interior R₁ y exterior R₂ tiene en su centro una pequeña partícula cargada con carga q. Suponiendo que la esfera no tiene carga neta y que está aislada calcule el potencial al que se encuentra y la carga que hay en sus superficies interior y exterior.

2 Solución

En la figura se muestra una sección transversal del sistema bajo estudio. Se trata de una esfera conductora de radio R₂, descargada y aislada, en cuyo interior hay un hueco esférico y concéntrico de radio R₁, que se encuentra vacío salvo en su centro O, donde hay situada una carga puntual de valor q.