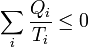Desigualdad de Clausius (GIE)
De Laplace
m |
|||
| Línea 113: | Línea 113: | ||
<center><math>\eta_ \leq \eta^\mathrm{rev}=1-\frac{T_F}{T_C}\qquad\qquad\mathrm{COP}_R\leq \mathrm{COP}_R^\mathrm{rev} = \frac{T_F}{T_C-T_F}\qquad\qquad \mathrm{COP}_{BC}\leq \mathrm{COP}_{BC}^\mathrm{rev} = \frac{T_C}{T_C-T_F}</math></center> | <center><math>\eta_ \leq \eta^\mathrm{rev}=1-\frac{T_F}{T_C}\qquad\qquad\mathrm{COP}_R\leq \mathrm{COP}_R^\mathrm{rev} = \frac{T_F}{T_C-T_F}\qquad\qquad \mathrm{COP}_{BC}\leq \mathrm{COP}_{BC}^\mathrm{rev} = \frac{T_C}{T_C-T_F}</math></center> | ||
==Caso de tres o más focos térmicos== | ==Caso de tres o más focos térmicos== | ||
| + | Consideremos ahora un caso más general de un dispositivo que absorbe calor en dos puntos del ciclo. Esto lo podemos modelar como una máquina en dos fases, absorbiéndose calor a una temperatura elevada y a una intermedia, de forma que | ||
| + | |||
| + | <center><math>Q_\mathrm{in1}=Q_C\qquad\qquad Q_\mathrm{in2}=\mathrm{out1}+Q_M\qquad\qquad Q_\mathrm{out2}=-Q_F</math></center> | ||
| + | |||
| + | Del teorema de Carnot para la primera máquina se deduce que | ||
| + | |||
| + | <center><math>Q_\mathrm{out1}\geq \frac{T_M}{T_C}Q_C</math></center> | ||
| + | |||
| + | y para la segunda | ||
| + | |||
| + | <center><math>-Q_F = Q_\mathrm{out2} \geq \frac{T_F}{T_M}Q_\mathrm{in2}= \frac{T_F}{T_M}\left(Q_\mathrm{out1}+Q_M\right)</math></center> | ||
| + | |||
| + | Combinando las dos relaciones queda | ||
| + | |||
| + | <center><math>-Q_F\geq \frac{T_F}{T_C}\left(Q_\mathrm{out1}+Q_M\right) \geq \frac{T_F}{T_M}\left(\frac{T_M}{T_C}Q_C+Q_M\right)</math></center> | ||
| + | |||
| + | y reordenando términos | ||
| + | |||
| + | <center><math>\frac{Q_C}{T_C}+\frac{Q_M}{T_M}+\frac{Q_F}{T_F}\leq 0</math></center> | ||
| + | |||
| + | Si etiquetamos los focos sin distinción de cuál es más caliente o más frío | ||
| + | |||
| + | <center><math>\frac{Q_1}{T_1}+\frac{Q_2}{T_2}+\frac{Q_3}{T_3}\leq 0</math></center> | ||
| + | |||
| + | cumpliéndose la igualdad solo en el caso de que el conjunto de los dos ciclos sea reversible (lo cual se cumple solo si todos y cada uno de los pasos son reversibles). | ||
| + | |||
| + | Vemos que se trata de una generalización inmediata de la desigualdad para dos focos térmicos. El mismo resultado se obtiene si el calor intermedio en lugar de entrar sale del sistema. | ||
| + | |||
| + | El proceso puede generalizarse a todos los pasos intermedios que queramos y con entradas y salidas arbitrarias de calor. El resultado es | ||
| + | |||
| + | <center><math>\sum_i \frac{Q_i}{T_i}\leq 0</math></center> | ||
| + | |||
| + | |||
==Desigualdad de Clausius== | ==Desigualdad de Clausius== | ||
[[Categoría:Segundo principio de la termodinámica (GIE)]] | [[Categoría:Segundo principio de la termodinámica (GIE)]] | ||
Revisión de 18:35 16 mar 2012
Contenido |
1 Introducción
Al introducir el Segundo Principio de la termodinámica, se formulan varios enunciados que, aunque poseen validez general, están expresados en términos de máquina térmica. Los más importantes de estos enunciados son:
- Enunciado de Kelvin-Planck
- No puede construirse un dispositivo que, operando en un ciclo, tenga como único resultado la absorción de calor de un solo foco y la producción de una cantidad equivalente de trabajo.
- Enunciado de Clausius
- Es imposible construir un dispositivo que, operando cíclicamente, tenga como único resultado el paso de calor de un foco frío a uno caliente.
- Teorema de Carnot
- El rendimiento de una máquina térmica irreversible que funcione entre dos temperaturas es siempre menor que el de una máquina térmica reversible que funcione entre las mismas temperaturas.
Estos tres enunciados son bastante “concretos” en cuanto a que hablan de procesos y dispositivos fácilmente interpretables. No obstante, el segundo principio de la termodinámica puede enunciarse de formas más abstractas que, si bien requieren un mayor esfuerzo para su interpretación, ponen de manifiesto de forma más clara la validez universal de esta ley.
Uno de estos enunciados, que es el que se trata en este artículo es la
- Desigualdad de Clausius
- Para todo proceso cíclico
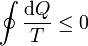
- cumpliéndose la desigualdad si el proceso es irreversible, y la igualdad si es reversible.
2 El caso de dos focos térmicos
Antes de enunciar de forma completa y rigurosa la desigualdad de Clausius, conviene presentar y analizar el caso más simple y importante de un sistema en contacto con solo dos focos de temperatura.
2.1 Caso de una máquina térmica
Supongamos un dispositivo que realiza un proceso cíclico, tomando calor de un foco caliente y cediéndolo a uno frío. Esto incluye el caso trivial en que no se realice trabajo alguno y se trate de un simple flujo de calor (incluso podría hacerse trabajo sobre el sistema).
De acuerdo con el teorema de Carnot el trabajo realizado en el proceso debe ser menor o igual que el que efectuaría una máquina reversible que operara ente las mismas temperaturas, por lo que

cumpliéndose la igualdad en el caso de que el ciclo sea reversible. Aplicando que el trabajo es la diferencia entre el calor que entra y el que sale, podemos escribir este resultado como una relación entre calores
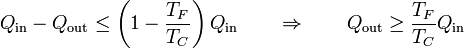
Esta relación nos dice que el calor expulsado es mayor del que expulsaría un ciclo reversible. Podemos reescribir esta ecuación en la forma
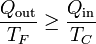
En lugar de la distinción entre calor que entra y calor que sale, podemos asignar el criterio de que todo el calor entra (siendo negativo cuando en realidad sale) y etiquetar cada uno de los dos por el foco al que corresponde. En este caso escribiríamos la identidad anterior como
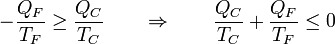
Si simplemente etiquetamos los focos por 1 y 2, sin distinción de cual tiene más temperatura nos queda la relación simétrica
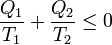
2.2 Caso de un refrigerador
Podemos operar de forma análoga para el caso de un refrigerador. En este caso, el teorema de Carnot nos dice que el calor que extraemos es menor del que absorberíamos con un refrigerador reversible
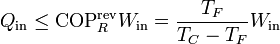
Expresando este resultado en términos solo de los calores
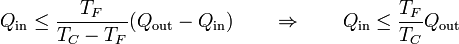
Teniendo en cuenta que en este caso el calor entra en el foco frío y sale en el caliente

y nos queda
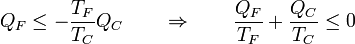
y etiquetando de nuevo los focos sin distinción de cuál es el frío y cual el caliente
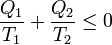
que es exactamente la misma relación que para una máquina térmica.
Si se hace el cálculo correspondiente para una bomba de calor, de nuevo se llega a la misma fórmula.
Por tanto, concluimos que para cualquier dispositivo o proceso cíclico que funcione entre solo dos focos térmicos se verifica la desigualdad
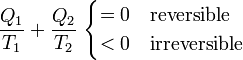
Esta sería la desigualdad de Clausius para dos focos térmicos, que más adelante generalizaremos.
2.3 Equivalencia con los otros enunciados
Si consideramos como punto de partida la desigualdad de Clausius para dos focos térmicos es sencillo llegar a otros resultados conocidos.
2.3.1 Con el enunciado de Clausius
Supongamos que tenemos calor que fluye de un foco a otro pasando por un sistema intermedio, para el cual
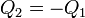
en este caso la desigualdad se reduce a
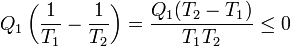
Si Q1 > 0 (el calor entra desde un foco a temperatura T1) para que se cumpla desigualdad debe ser T2 < T1, es decir el calor debe ir del foco caliente al frío. Si fuera al contrario resultaría un valor positivo. Por tanto de la desigualdad de Clausius se deduce el enunciado de Clausius
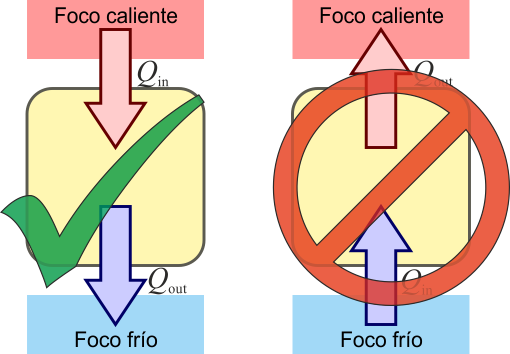
2.3.2 Con el enunciado de Kelvin-Planck
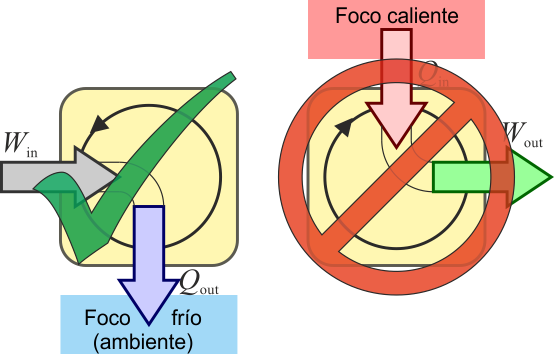
El que se deduzca el enunciado de Clausius implica que también se deduce el enunciado de Kelvin-Planck, pero podemos demostrarlo directamente. Supongamos un sistema que intercambia calor con un solo foco térmico, de forma que
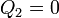
Esto reduce la desigualdad de Clausius a
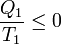
que implica que
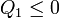
es decir, que un sistema que intercambia calor con un solo foco, solo puede hacerlo transformando trabajo en calor (ya que el calor de salida es negativo), nunca al contrario. Este es el enunciado de Kelvin-Planck
2.3.3 Con el teorema de Carnot
Partiendo de la desigualdad de Clausius basta ccn seguir los pasos del primer apartado en sentido inverso para llegar al teorema de Carnot en todas sus variantes
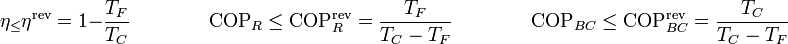
3 Caso de tres o más focos térmicos
Consideremos ahora un caso más general de un dispositivo que absorbe calor en dos puntos del ciclo. Esto lo podemos modelar como una máquina en dos fases, absorbiéndose calor a una temperatura elevada y a una intermedia, de forma que
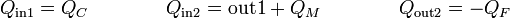
Del teorema de Carnot para la primera máquina se deduce que
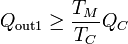
y para la segunda
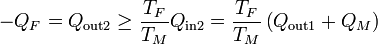
Combinando las dos relaciones queda
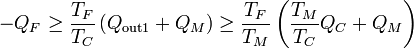
y reordenando términos
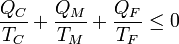
Si etiquetamos los focos sin distinción de cuál es más caliente o más frío
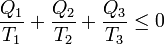
cumpliéndose la igualdad solo en el caso de que el conjunto de los dos ciclos sea reversible (lo cual se cumple solo si todos y cada uno de los pasos son reversibles).
Vemos que se trata de una generalización inmediata de la desigualdad para dos focos térmicos. El mismo resultado se obtiene si el calor intermedio en lugar de entrar sale del sistema.
El proceso puede generalizarse a todos los pasos intermedios que queramos y con entradas y salidas arbitrarias de calor. El resultado es