Calentamiento de agua con una resistencia
De Laplace
| Línea 36: | Línea 36: | ||
<center><math>V_2 = \frac{0.50\times 8.314\times 373}{0.018\times 10^5}\,\mathrm{m}^3 = 0.861\,\mathrm{m}^3</math></center> | <center><math>V_2 = \frac{0.50\times 8.314\times 373}{0.018\times 10^5}\,\mathrm{m}^3 = 0.861\,\mathrm{m}^3</math></center> | ||
| + | |||
| + | Vemos que volumen se multiplica por 1700, y para ocupar todo ese espacio con vapor, es necesario desalojar la cantidad correspondiente de aire, venciendo a la presión externa. | ||
| + | |||
| + | El trabajo realizado sobre el gas (de signo contrario al realizado por el gas) vale | ||
| + | |||
| + | <center><math>W=-p\,\Delta V = -10^5(0.861-0.0005)\,\mathrm{J} = -86.1\,\mathrm{kJ}</math></center> | ||
==Entalpía y energía== | ==Entalpía y energía== | ||
==Tiempo necesario== | ==Tiempo necesario== | ||
[[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | [[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | ||
Revisión de 13:49 2 mar 2012
Contenido |
1 Enunciado
En una cámara con un émbolo móvil se coloca 500 cm³ de agua a 300 K. El exterior se encuentra a una presión de 100 kPa. Se le comunica lentamente calor al agua hasta que se evapora por completo.
- Calcule el calor necesario para que se realice este proceso.
- Halle el trabajo que se realiza sobre el agua.
- Calcule la variación en la entalpía y en la energía interna del agua.
- Suponga que el calentamiento se produce mediante una resistencia eléctrica a una tensión de 220 V por la que pasa una corriente de 2 A. ¿Cuánto tiempo tarda en realizarse el proceso? En este caso, la energía entra en el sistema en forma de calor o de trabajo?
2 Calor
Al ser el émbolo móvil, todos los procesos son a presión exterior constante. Suponiendo que ocurre cuasiestáticamente, esta presión será también la interior.
Para vaporizar el agua primero hay que llevarla a 100°C, lo que requiere una cantidad calor
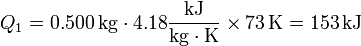
A continuación hay que comunicarle el calor necesario para evaporar el agua

El calor total necesario será la suma de estos dos

3 Trabajo
El sistema realiza trabajo ya que se produce un incremento de volumen, pues el vapor ocupa mucho más espacio que el agua líquida.
Inicialmente el sistema ocupa
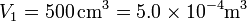
y tras la evaporación, suponiendo que se comporta como un gas ideal
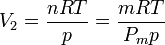
Sustituyendo los valores numéricos
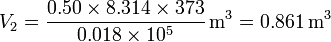
Vemos que volumen se multiplica por 1700, y para ocupar todo ese espacio con vapor, es necesario desalojar la cantidad correspondiente de aire, venciendo a la presión externa.
El trabajo realizado sobre el gas (de signo contrario al realizado por el gas) vale






