Mezcla de hielo y vapor de agua
De Laplace
| Línea 70: | Línea 70: | ||
<center><math>Q_{2c} = m_v\,c_a(T-T_b) = 0.909\times 4.18\times(T-373)\,\mathrm{kJ} = 3.80(T-373)\,\mathrm{kJ}</math></center> | <center><math>Q_{2c} = m_v\,c_a(T-T_b) = 0.909\times 4.18\times(T-373)\,\mathrm{kJ} = 3.80(T-373)\,\mathrm{kJ}</math></center> | ||
| + | Llevando todo esto a la ecuación | ||
| + | <center><math>Q_1 + Q_2 =0\,</math></center> | ||
| + | |||
| + | nos queda la ecuación para la temperatura | ||
| + | |||
| + | <center><math>10.6+167+2.09(T-273)-28.5-2052+3.80(T-373)=0\qquad\Rightarrow\qquad T = 693\,\mathrm{K}</math></center> | ||
| + | |||
| + | pero este resultado es '''absurdo'''. No es posible que la temperatura final del sistema sea mucho mayor que las dos de partidas (mucho mayor en este caso) y además incompatible con la hipótesis de que el estado final es agua (que debe estar entre 273 y 373 kelvin). | ||
| + | |||
| + | No es posible, por tanto, que el estado final sea todo agua a una temperatura intermedia. | ||
| + | |||
| + | Lo que ocurre realmente es que , puesto que la entalpía de ebullición del agua es muy elevada, solo con licuar una parte del vapor ya es suficiente para llevar el hielo al estado de agua a 100°C. Una vez ahí, ya se ha alcanzado el equilibrio térmico entre agua a 100°C y vapor de agua a la misma temperatura. | ||
| + | |||
| + | La incógnita entonces es saber cuánta masa de vapor se licúa. El cálculo es ahora | ||
| + | |||
| + | ;Calentamiento del hielo: | ||
| + | |||
| + | <center><math>Q_{1a} = m_hc_h(T_f-T_h) =0.5\times2.11\times(273-263)\,\mathrm{kJ}= 10.6\,\mathrm{kJ}</math></center> | ||
| + | |||
| + | ;Fusión del hielo: | ||
| + | |||
| + | <center><math>Q_{1b} = m_h\,\Delta h_f = 0.5\times 334\,\mathrm{kJ} = 167\,\mathrm{kJ}</math></center> | ||
| + | |||
| + | ;Calentamiento del agua fría hasta los 100°C: | ||
| + | |||
| + | <center><math>Q_{1c} = m_h\,c_a(T_b-T_f) = 0.5\times 4.18\times(373-273)\,\mathrm{kJ} = 209\,\mathrm{kJ}</math></center> | ||
| + | |||
| + | ;Enfriamiento del vapor: | ||
| + | |||
| + | <center><math>Q_{2a} = m_v c_{va}(T_b-T_v) = 0.909\times 2.09\times(373-388)\,\mathrm{kJ}=-28.5\,\mathrm{kJ}</math></center> | ||
| + | |||
| + | ;Licuación parcial del vapor: | ||
| + | |||
| + | <center><math>Q_{2b} = -m\,\Delta h_b = -2257m\,\mathrm{kJ}</math></center> | ||
| + | |||
| + | y nos queda ahora la ecuación | ||
| + | |||
| + | <center><math>10.6+167+209-28.5-2257m=0\qquad\Rightarrow\qquad m = 0.072\,\mathrm{kg} = 72\,\mathrm{g}</math></center> | ||
| + | |||
| + | es decir, de los 909 gramos de vapor solo se licúan 72. El resto permanece en estado de vapor. El volumen que ocupa el vapor restante es | ||
| + | |||
| + | <center><math>n = \frac{909-72}{28.96}\,\mathrm{mol}=28.9\,ºmathrm{mol}\qquad\qquad V= \frac{28.9\times 8.314\times 373}{101300}\,\mathrm{m}^3 = 0.88\,\mathrm{m}^3</math></center> | ||
| + | |||
| + | mientras que tenemos 572 g de agua que ocupan un volumen correspondiente en cm³ | ||
[[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | [[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | ||
Revisión de 10:33 27 feb 2012
1 Enunciado
En un recipiente a presión constante de 101.3 kPa, se ponen en contacto 1.0 m³ de vapor de agua a 115 °C con 500 g de hielo a −10 °C. Determine la temperatura final del sistema.
2 Solución
Al poner en contacto las dos fases se producirá un flujo de calor desde el vapor al hielo. Uno se irá enfriando a medida que el otro se calienta, quedando el sistema en un estado final en que ambos subsistemas tienen la misma temperatura.
Suponemos de entrada que el estado final será un punto intermedio en el que las dos fases se encuentran en el estado de agua líquida.
Para convertir el hielo en agua a una temperatura T es necesario proporcionar un calor
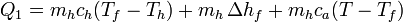
donde:
- el primer término, mhch(Tf − Th), representa el calor necesario para llevar el hielo desde su temperatura inicial, Th a la temperatura de fusión Tf-
- el segundo término,
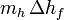 , es el calor preciso para fundir el hielo
, es el calor preciso para fundir el hielo
- el tercer término, mhca(T − Tf), es el calor que hace falta para elevar la temperatura del agua desde el punto de fusión hasta la temperatura final.
De la misma manera, para el enfriamiento del vapor escribimos
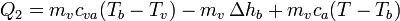
siendo Tb la temperatura de ebullición del agua. Los valores numéricos que usaremos para las constantes son, para los calores específicos
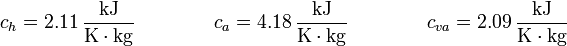
y para las entalpías de cambio de fase

Las temperaturas que aparecen en las fórmulas anteriores valen

La masa de vapor de agua la calculamos a partir de su presión, volumen y temperatura
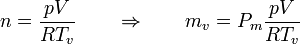
siendo

el peso molecular medio del aire. Esto nos da la masa

Con estos datos obtenemos los siguientes calores:
- Calentamiento del hielo
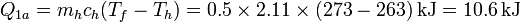
- Fusión del hielo

- Calentamiento del agua fría
- Estando la temperatura expresada en kelvins
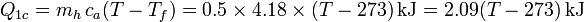
- Enfriamiento del vapor
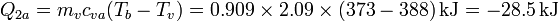
- Licuación del vapor

- Enfriamiento del agua caliente
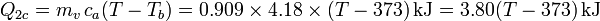
Llevando todo esto a la ecuación
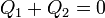
nos queda la ecuación para la temperatura
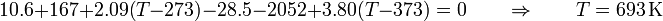
pero este resultado es absurdo. No es posible que la temperatura final del sistema sea mucho mayor que las dos de partidas (mucho mayor en este caso) y además incompatible con la hipótesis de que el estado final es agua (que debe estar entre 273 y 373 kelvin).
No es posible, por tanto, que el estado final sea todo agua a una temperatura intermedia.
Lo que ocurre realmente es que , puesto que la entalpía de ebullición del agua es muy elevada, solo con licuar una parte del vapor ya es suficiente para llevar el hielo al estado de agua a 100°C. Una vez ahí, ya se ha alcanzado el equilibrio térmico entre agua a 100°C y vapor de agua a la misma temperatura.
La incógnita entonces es saber cuánta masa de vapor se licúa. El cálculo es ahora
- Calentamiento del hielo
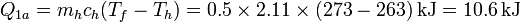
- Fusión del hielo

- Calentamiento del agua fría hasta los 100°C
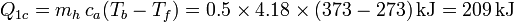
- Enfriamiento del vapor
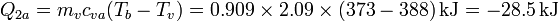
- Licuación parcial del vapor
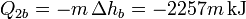
y nos queda ahora la ecuación

es decir, de los 909 gramos de vapor solo se licúan 72. El resto permanece en estado de vapor. El volumen que ocupa el vapor restante es

mientras que tenemos 572 g de agua que ocupan un volumen correspondiente en cm³





