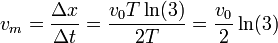Cálculo de velocidad media

(Diferencias entre revisiones)

última version al 23:22 1 feb 2012

Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley

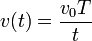
$v(t) = \frac{v_0T}{t}$

¿Cuánto vale la velocidad media entre $t = T$ y $t = 3 T$ ?

La velocidad media en un intervalo es igual al cociente entre el desplazamiento realizado en un intervalo y la duración de este intervalo

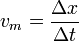
$v_m = \frac{\Delta x}{\Delta t}$

La duración del intervalo es la diferencia entre el instante inicial final y el inicial

Δ t = 3 T - T = 2 T

mientras que el desplazamiento es la suma de los desplazamientos infinitesimales, y por tanto igual a la integral de la velocidad instantánea

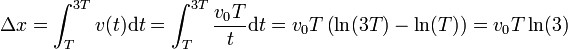
$\Delta x = \int_T^{3T} v(t)\mathrm{d}t = \int_T^{3T}\frac{v_0T}{t}\mathrm{d}t = v_0T\left(\ln(3T)-\ln(T)\right)=v_0T\ln(3)$

La velocidad media vale entonces

$v_m = \frac{\Delta x}{\Delta t} = \frac{v_0T\ln(3)}{2T}=\frac{v_0}{2}\ln(3)$

@@ Línea 23: / Línea 23: @@
 <center><math>v_m = \frac{\Delta x}{\Delta t} = \frac{v_0T\ln(3)}{2T}=\frac{v_0}{2}\ln(3)</math></center>
+[[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]]
 [[Categoría:Problemas de cinemática de la partícula (GIE)]]