Resorte con rozamiento seco
De Laplace
(→Posición de la segunda parada) |
|||
| Línea 20: | Línea 20: | ||
La única fuerza que afecta al movimiento es la fuerza elástica debida al resorte. Además de esta actúan el peso y la reacción normal del plano, pero éstas se anulan mutuamente y no producen movimiento. | La única fuerza que afecta al movimiento es la fuerza elástica debida al resorte. Además de esta actúan el peso y la reacción normal del plano, pero éstas se anulan mutuamente y no producen movimiento. | ||
| - | En la posición inicial el muelle está comprimido una cierta cantidad y a partir de ahí se suelta desde el reposo. El movimiento que describe la masa es un movimiento armónico simple alrededor de la posición de equilibrio | + | En la posición inicial el muelle está comprimido una cierta cantidad y a partir de ahí se suelta desde el reposo. El movimiento que describe la masa es un movimiento armónico simple alrededor de la posición de equilibrio. |
| + | [[Archivo:rozamiento-seco-resorte-01.png|right]] | ||
| + | |||
| + | En el instante inicial, la partícula se encuentra en reposo a una distancia <math>b</math> del punto de equilibrio. La amplitud de las oscilaciones que describe tendrán entonces esta amplitud | ||
| + | |||
| + | <center><math>A = b\,</math></center> | ||
| + | |||
| + | La partícula comienza a moverse en un punto a una distancia b del punto de equilibrio, se acelera hacia éste, pasa por el punto de equilibrio con velocidad máxima y a partir de ahí comienza a frenarse, llegando a detenerse cuando se encuentra en el punto simétrico respecto del central. Por tanto, la máxima distancia del origen la alcanza en | ||
| + | |||
| + | <center><math>x_\mathrm{max} = l_0+b\,</math></center> | ||
| + | |||
| + | A partir de ahí retrocede, volviendo a detenerse en la posición inicial, reiniciándose el proceso. | ||
| + | |||
| + | <!-- | ||
<center><math>x = l_0 + A\cos(\omega t-\varphi)\qquad\qquad v=\frac{\mathrm{d}x}{\mathrm{d}t}=-A\omega\,\mathrm{sen}(\omega t-\varphi)\qquad\qquad\omega = \sqrt{\frac{k}{m}}</math></center> | <center><math>x = l_0 + A\cos(\omega t-\varphi)\qquad\qquad v=\frac{\mathrm{d}x}{\mathrm{d}t}=-A\omega\,\mathrm{sen}(\omega t-\varphi)\qquad\qquad\omega = \sqrt{\frac{k}{m}}</math></center> | ||
| Línea 27: | Línea 40: | ||
<center><math>\left\{\begin{array}{rcl} x(t=0) & = & l_0-b = l_0+A\cos(\varphi) \\ v(t=0) & = & 0 =-A\omega\,\mathrm{sen}(-\varphi)\end{array}\right.\qquad\Rightarrow\qquad A=b\,\qquad\varphi = \pi</math></center> | <center><math>\left\{\begin{array}{rcl} x(t=0) & = & l_0-b = l_0+A\cos(\varphi) \\ v(t=0) & = & 0 =-A\omega\,\mathrm{sen}(-\varphi)\end{array}\right.\qquad\Rightarrow\qquad A=b\,\qquad\varphi = \pi</math></center> | ||
| - | |||
| - | |||
De estas ecuaciones podría tomarse como solución que <math>A=-b</math>, <math>\varphi=0</math>, pero, aunque el resultado final es el mismo, debemos procurar tomar la amplitud como una cantidad positiva. Lo que nos dice la constante de fase <math>\varphi=\pi</math> es que la oscilación comienza en el punto de mínima elongación en lugar del de máxima. | De estas ecuaciones podría tomarse como solución que <math>A=-b</math>, <math>\varphi=0</math>, pero, aunque el resultado final es el mismo, debemos procurar tomar la amplitud como una cantidad positiva. Lo que nos dice la constante de fase <math>\varphi=\pi</math> es que la oscilación comienza en el punto de mínima elongación en lugar del de máxima. | ||
| Línea 39: | Línea 50: | ||
<center><math>x_\mathrm{max} = l_0+b\,</math></center> | <center><math>x_\mathrm{max} = l_0+b\,</math></center> | ||
| - | + | --> | |
Numéricamente en nuestro caso | Numéricamente en nuestro caso | ||
<center><math>x_\mathrm{max}=150\,\mathrm{mm}+50\,\mathrm{mm} = 200\,\mathrm{mm}</math></center> | <center><math>x_\mathrm{max}=150\,\mathrm{mm}+50\,\mathrm{mm} = 200\,\mathrm{mm}</math></center> | ||
| + | <!-- | ||
Este resultado se expresa de forma sencilla con palabras: tenemos el muelle en equilibrio, lo comprimimos 50mm respecto a la posición de equilibrio; el máximo alejamiento se da cuando el estiramiento del muelle es igual a la compresión inicial. | Este resultado se expresa de forma sencilla con palabras: tenemos el muelle en equilibrio, lo comprimimos 50mm respecto a la posición de equilibrio; el máximo alejamiento se da cuando el estiramiento del muelle es igual a la compresión inicial. | ||
| - | + | --> | |
[[Archivo:rozamiento-seco-resorte-02.png|right]] | [[Archivo:rozamiento-seco-resorte-02.png|right]] | ||
Revisión de 17:17 22 ene 2012
Contenido |
1 Enunciado
Se tiene una masa 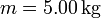 atada a un resorte de constante
atada a un resorte de constante  y longitud en reposo
y longitud en reposo  . La masa reposa sobre una superficie horizontal sobre la que existe un pequeño coeficiente de rozamiento μ = 0.10. El muelle se comprime una cantidad
. La masa reposa sobre una superficie horizontal sobre la que existe un pequeño coeficiente de rozamiento μ = 0.10. El muelle se comprime una cantidad 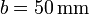 respecto a su posición de equilibrio.
respecto a su posición de equilibrio.
- Despreciando en primer lugar el rozamiento, determine la máxima distancia de la pared a la que llega la masa.
- Teniendo en cuenta el rozamiento, ¿cuánto vale la distancia de máximo alejamiento?
- Al volver a comprimirse el muelle, la masa no retorna a su posición inicial. ¿A qué distancia de la pared se detiene instantáneamente?
- ¿Al cabo de cuantas oscilaciones se detiene del todo? ¿Dónde se queda parada?
2 Máxima distancia sin rozamiento
Cuando no hay rozamiento, el análisis es sencillo.
Tenemos un movimiento rectilíneo, por lo que podemos emplear cantidades escalares.
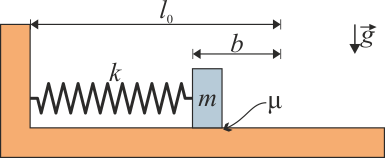
Si llamamos x a la distancia desde la pared, la ecuación de movimiento para la masa la da la ley de Hooke,
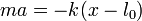
La única fuerza que afecta al movimiento es la fuerza elástica debida al resorte. Además de esta actúan el peso y la reacción normal del plano, pero éstas se anulan mutuamente y no producen movimiento.
En la posición inicial el muelle está comprimido una cierta cantidad y a partir de ahí se suelta desde el reposo. El movimiento que describe la masa es un movimiento armónico simple alrededor de la posición de equilibrio.
En el instante inicial, la partícula se encuentra en reposo a una distancia b del punto de equilibrio. La amplitud de las oscilaciones que describe tendrán entonces esta amplitud
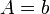
La partícula comienza a moverse en un punto a una distancia b del punto de equilibrio, se acelera hacia éste, pasa por el punto de equilibrio con velocidad máxima y a partir de ahí comienza a frenarse, llegando a detenerse cuando se encuentra en el punto simétrico respecto del central. Por tanto, la máxima distancia del origen la alcanza en
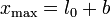
A partir de ahí retrocede, volviendo a detenerse en la posición inicial, reiniciándose el proceso.
Numéricamente en nuestro caso
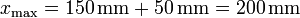
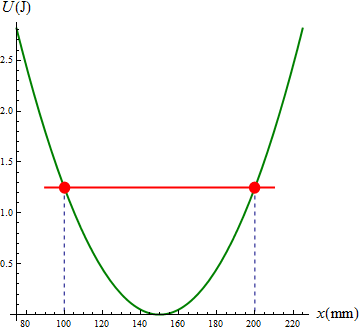
A este resultado se puede llegar también de manera sencilla empleando consideraciones energéticas. Para cualquier posición de la masa, ésta tiene una energía potencial elástica proporcional a la elongación al cuadrado
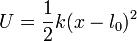
En ausencia de rozamiento, la energía mecánica se conserva, por lo que podemos igualar la energía mecánica inicial con la final. En el estado inicial, la velocidad de la masa es nula, por lo que su energía cinética vale 0, toda la energía mecánica es potencial y la partícula se halla en un punto de retorno.
En la posición de máximo alejamiento, la velocidad vuelve a ser nula, por lo que la partícula se encuentra en el otro punto de retorno, en el que la energía mecánica vuelve a ser solo potencial. Por tanto
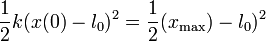
de donde
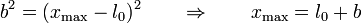
La ecuación posee otra solución l0 − b correspondiente a la posición inicial.
3 Máxima distancia con rozamiento
Cuando el bloque roza con el suelo aparece una fuerza adicional. Esta nueva fuerza es la de rozamiento dinámico, proporcional a la fuerza normal aplicada. La fuerza normal aplicada es igual al peso en módulo y dirección, y sentido opuesto. Por tanto
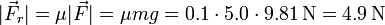
Esta fuerza es constante en módulo y dirección, pero no en sentido. La fuerza de rozamiento dinámico siempre se opone a la velocidad relativa, por lo tanto, cuando la partícula avance hacia la derecha, la fuerza de rozamiento irá hacia la izquierda y viceversa.
Para determinar la posición de máximo alejamiento debemos considerar una parte del movimiento en que x es siempre creciente, por lo que la fuerza de rozamiento irá siempre en el sentido de x decreciente y la ecuación de movimiento para la masa se escribe

Esta ecuación es de nuevo la de un oscilador armónico, pero con un punto de equilibrio diferente del anterior. Podemos obtener la nueva posición de equilibrio viendo para que valor de x la aceleración se anula, o bien agrupando términos.
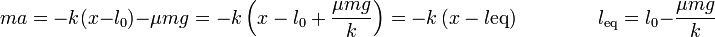
Puesto que, como antes, parte del reposo, el movimiento resultante es media oscilación alrededor del nuevo punto de equilibrio
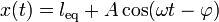
Aplicando de nuevo las condiciones iniciales
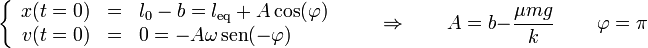
Obtenemos la ecuación horaria
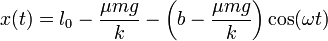
Obsérvese que no solo cambia la posición de equilibrio, sino también la amplitud de las oscilaciones, pues el nuevo punto de equilibrio está más cerca de la posición inicial.
El nuevo alcance máximo lo obtenemos haciendo t = T / 2 = π / ω
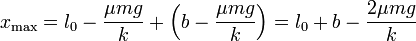
con valor numérico

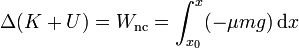
Por ser esta fuerza constante, puede salir de la integral y nos queda

El máximo alcance se da cuando la energía cinética vuelve a ser cero. Esto nos da la ecuación para el balance energético
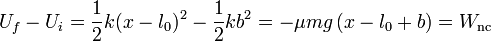
Llegamos así a la ecuación de segundo grado
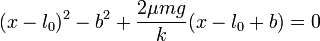
cuyas soluciones son

La primera es la posición inicial. La segunda es la posición de máximo alcance.
Gráficamente, en este caso la energía mecánica disminuye linealmente con la posición, por lo que en lugar de una recta horizontal tenemos una oblicua. Donde esta recta corta a la parábola es la posición de máximo alcance.
4 Posición de la segunda parada
Una vez que llega al punto de máximo alejamiento, la partícula retorna.
Si no existe rozamiento, la posición de mínima distancia es la misma que la inicial. El movimiento armónico continúa indefinidamente, oscilando entre la posición mínima y la máxima.
Cuando hay rozamiento, en cambio, las oscilaciones se van atenuando progresivamente. La razón es que la fuerza de rozamiento siempre se opone a la velocidad relativa. Esto quiere decir que en el retorno la ecuación de movimiento es
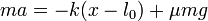
donde ha cambiado el signo de la fuerza de rozamiento, respecto al camino de ida. Esto nos da una nueva posición de equilibrio, diferente de la anterior
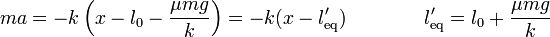
El movimiento en esta media oscilación es de nuevo armónico
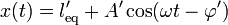
donde ahora nuestros datos iniciales no son los correspondientes a t = 0, sino los calculados en el apartado anterior para la segunda posición de retorno, para la cual t = T / 2 = π / ω
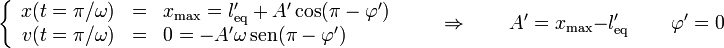
La posición mínima será la correspondiente al siguiente medio periodo
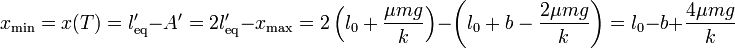
con el valor numérico
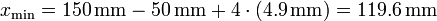
A partir de ahí la partícula vuelve a avanzar, reduciéndose aun más la distancia máxima (porque parte de una posición más cercana a la de equilibrio. Los sucesivos máximos son
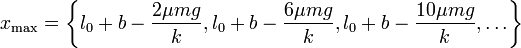
de valores

mientras que los sucesivos mínimos se hallan en
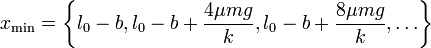
con valores
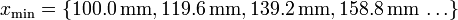
Un rápido examen a estos valores muestra que llega un punto en que son imposibles, pues resulta un mínimo mayor que un máximo. La razón es que antes de llegar a esa situación la partícula se ha detenido definitivamente como veremos en la sección siguiente.