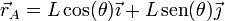Movimiento de un sistema biela-manivela
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Un sistema biela-manivela está formado por: una barra fija (el ''eje'' “1”); una barra (la ''manivela'' “0”) de longitud <math>L</math>, a…') |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Un sistema biela-manivela está formado por: una barra fija (el ''eje'' “1”); una barra (la ''manivela'' “0”) de longitud <math>L</math>, articulada en el punto O del eje y que forma un ángulo <math>\theta(t)</math> con él; y una segunda barra | + | Un sistema biela-manivela está formado por: una barra fija (el ''eje'' “1”); una barra (la ''manivela'' “0”) de longitud <math>L</math>, articulada en el punto O del eje y que forma un ángulo <math>\theta(t)</math> con él; y una segunda barra (la ''biela'' “2”), también de longitud <math>L</math>, articulada en el punto A de la manivela y cuyo segundo extremo B está obligado a deslizar por el eje. |
| - | (la ''biela'' “2”), también de longitud <math>L</math>, articulada en el punto A de la manivela y cuyo segundo extremo B está obligado a deslizar por el eje. | + | |
# Halle las velocidades de los puntos A y B de la biela. | # Halle las velocidades de los puntos A y B de la biela. | ||
| Línea 11: | Línea 10: | ||
==Velocidades de A y B== | ==Velocidades de A y B== | ||
| + | ===Velocidad de A=== | ||
| + | El punto A describe, respecto al eje fijo, un movimiento circular. Su posición en cada instante es | ||
| + | |||
| + | <center><math>\vec{r}_A = L\cos(\theta)\vec{\imath}+L\,\mathrm{sen}(\theta)\vec{\jmath}</math></center> | ||
| + | |||
| + | |||
==Velocidad angular== | ==Velocidad angular== | ||
==Posición del CIR== | ==Posición del CIR== | ||
==Aplicación numérica== | ==Aplicación numérica== | ||
[[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | [[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | ||
Revisión de 21:50 11 ene 2012
Contenido |
1 Enunciado
Un sistema biela-manivela está formado por: una barra fija (el eje “1”); una barra (la manivela “0”) de longitud L, articulada en el punto O del eje y que forma un ángulo θ(t) con él; y una segunda barra (la biela “2”), también de longitud L, articulada en el punto A de la manivela y cuyo segundo extremo B está obligado a deslizar por el eje.
- Halle las velocidades de los puntos A y B de la biela.
- Determine la velocidad angular de la biela respecto al eje.
- Localice el centro instantáneo de rotación (CIR) de la biela respecto al eje.
- Suponga el caso
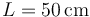y que en un instante dado tg(θ) = 0.75 siendo 
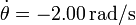. Calcule la velocidades respecto al eje de los puntos A y B de la biela, su velocidad angular y las coordenadas del CIR.
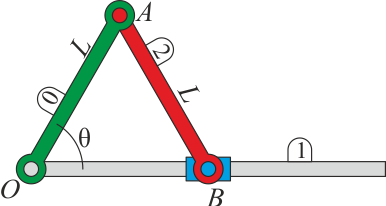
2 Velocidades de A y B
2.1 Velocidad de A
El punto A describe, respecto al eje fijo, un movimiento circular. Su posición en cada instante es
