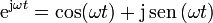Problemas de Movimiento oscilatorio (GIC)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Pelota que bota y bota== Un balón que se ha dejado caer desde una altura de 4 m choca con el suelo con una colisión perfectamente elástica. Suponiendo que no se pierde …') |
(→Pelota que bota y bota) |
||
| Línea 2: | Línea 2: | ||
Un balón que se ha dejado caer desde una altura de 4 m choca con el suelo con una colisión perfectamente elástica. Suponiendo que no se | Un balón que se ha dejado caer desde una altura de 4 m choca con el suelo con una colisión perfectamente elástica. Suponiendo que no se | ||
pierde energía debido a la resistencia del aire, demuestre que el movimiento es periódico. Determine el periodo del movimiento, ¿Es éste un movimiento armónico simple? | pierde energía debido a la resistencia del aire, demuestre que el movimiento es periódico. Determine el periodo del movimiento, ¿Es éste un movimiento armónico simple? | ||
| + | |||
| + | ==[[Solución general del MAS]]== | ||
| + | La solución general de la ecuación de movimiento | ||
| + | |||
| + | <center><math>m\frac{\mathrm{d}^2x}{\mathrm{d}t^2} = -k x</math></center> | ||
| + | |||
| + | es de la forma | ||
| + | |||
| + | <center><math>x = a \cos(\omega t)+b\,\mathrm{sen}\,(\omega t)</math>{{qquad}}<math>\omega=\sqrt{\frac{k}{m}}</math></center> | ||
| + | |||
| + | con <math>a</math> y <math>b</math> dos constantes dependientes de las condiciones iniciales. | ||
| + | |||
| + | # Halle el valor de las constantes <math>a</math> y <math>b</math> si la posición inicial de la partícula es <math>x_0</math> y su velocidad inicial es <math>v_0</math>. | ||
| + | # Demuestre que la ecuación horaria <math>x = A \cos\left(\omega t+\phi\right)</math> es también solución de la misma ecuación de movimiento. Empleando relaciones trigonométricas, deduzca la relación entre las constantes <math>\{A,\phi\}</math> y las constantes <math>\{a,b\}</math>. Exprese <math>A</math> y <math>\phi</math> en función de la posición y la velocidad iniciales, <math>x_0</math> y <math>v_0</math>. | ||
| + | # Calcule la velocidad de la partícula para cualquier instante en función de la posición y velocidad iniciales. | ||
| + | # Demuestre que la cantidad <math>E=mv^2/2+kx^2/2</math> no depende del tiempo. ¿Cuánto vale en función de las condiciones iniciales? | ||
| + | # Demuestre que <math>x = \mathrm{e}^{\mathrm{j}\omega t}</math>, con <math>\mathrm{j}=\mathrm{i}=\sqrt{-1}</math>, la unidad imaginaria, es una solución particular de la ecuación de movimiento. Aplicando los resultados anteriores, demuestre la relación | ||
| + | |||
| + | <center><math>\mathrm{e}^{\mathrm{j}\omega t}=\cos(\omega t)+\mathrm{j}\,\mathrm{sen}\,(\omega t)</math></center> | ||
Revisión de 11:47 10 ene 2012
1 Pelota que bota y bota
Un balón que se ha dejado caer desde una altura de 4 m choca con el suelo con una colisión perfectamente elástica. Suponiendo que no se pierde energía debido a la resistencia del aire, demuestre que el movimiento es periódico. Determine el periodo del movimiento, ¿Es éste un movimiento armónico simple?
2 Solución general del MAS
La solución general de la ecuación de movimiento
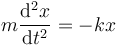
es de la forma
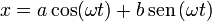
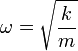
con a y b dos constantes dependientes de las condiciones iniciales.
- Halle el valor de las constantes a y b si la posición inicial de la partícula es x0 y su velocidad inicial es v0.
- Demuestre que la ecuación horaria
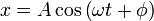es también solución de la misma ecuación de movimiento. Empleando relaciones trigonométricas, deduzca la relación entre las constantes {A,φ} y las constantes {a,b}. Exprese A y φ en función de la posición y la velocidad iniciales, x0 y v0.
- Calcule la velocidad de la partícula para cualquier instante en función de la posición y velocidad iniciales.
- Demuestre que la cantidad E = mv2 / 2 + kx2 / 2 no depende del tiempo. ¿Cuánto vale en función de las condiciones iniciales?
- Demuestre que x = ejωt, con
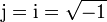, la unidad imaginaria, es una solución particular de la ecuación de movimiento. Aplicando los resultados anteriores, demuestre la relación
