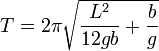Péndulo compuesto
De Laplace
(→Ecuaciones de movimiento) |
(→Ecuaciones de movimiento) |
||
| Línea 27: | Línea 27: | ||
y el momento del peso | y el momento del peso | ||
| - | <center><math>\vec{M}_O = \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ b\,\mathrm{sen}(\theta) & 0 & b\cos(\theta) \\ 0 & 0 & -Mg\end{ | + | <center><math>\vec{M}_O = \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ b\,\mathrm{sen}(\theta) & 0 & b\cos(\theta) \\ 0 & 0 & -Mg\end{matrix}\right| = Mgb\,\mathrm{sen}(\theta)\vec{\jmath}</math></center> |
El momento cinético es el correspondiente a un eje permanente de rotación. | El momento cinético es el correspondiente a un eje permanente de rotación. | ||
| Línea 41: | Línea 41: | ||
<center><math>I_O = I' + Md^2 = \frac{1}{12}MH^2 + M b^2</math></center> | <center><math>I_O = I' + Md^2 = \frac{1}{12}MH^2 + M b^2</math></center> | ||
| - | Derivando respecto | + | Derivando respecto al tiempo el momento cinético |
| + | |||
| + | <center><math>\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t} = -I_O\ddot{\theta}\vec{\jmath}</math></center> | ||
| + | |||
| + | Si igualamos esta derivada al momento de las fuerzas queda la ecuación de movimiento | ||
| + | |||
| + | <center><math>I_0\ddot{\theta}=-Mgb\,\mathrm{sen}(\theta)</math></center> | ||
| + | |||
| + | Si el ángulo de desviación es pequeño puede aproximarse el seno por su argumento y escribirse | ||
| + | |||
| + | <center><math>\ddot{\theta}=-\frac{Mgb}{I_O}\theta</math></center> | ||
| + | |||
| + | que es la ecuación de un oscilador armónico de frecuencia angular | ||
| + | |||
| + | <center><math>\omega = \sqrt{\frac{Mgb}{I_O}}</math></center> | ||
| + | |||
| + | a la cual corresponde un periodo | ||
| + | |||
| + | <center><math>T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{I_O}{Mgb}}</math></center> | ||
| + | |||
| + | Sustituyendo el valor del momento de inercia queda | ||
| + | |||
| + | <center><math>T = 2\pi\sqrt{\frac{L^2}{12gb}+\frac{b}{g}}</math></center> | ||
==Periodo== | ==Periodo== | ||
==Fuerza de reacción== | ==Fuerza de reacción== | ||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
Revisión de 21:38 5 ene 2012
Contenido |
1 Enunciado
Se tiene un péndulo compuesto consistente en una barra de longitud H y masa M suspendida por un punto situado a una distancia b del centro de la barra (b < H / 2). Suponiendo que la barra se desvía un ángulo pequeño $\theta_0$ respecto de la vertical y a partir de ahí se suelta:
- Determine el periodo de oscilación de la barra
- Calcule la fuerza ejercida sobre el punto de anclaje cuando la barra pasa por la vertical en su oscilación.
2 Ecuaciones de movimiento
Determinaremos en primer lugar la ecuación de movimiento para el ángulo θ que la barra forma con la vertical.
La barra constituye un sólido rígido sometido a dos fuerzas:
- Su peso,
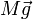
- La fuerza de reacción, Φ ejercida por el soporte
La suma de estas dos fuerzas produce la aceleración del centro de masas
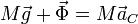
La suma de los momentos produce la variación del momento cinético de la partícula
siendo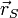 
la posición del soporte respecto al punto de referencia que tomemos. La fuerza de reacción es en sí misma una incógnita del problema. Podemos eliminarla de esta ecuación si elegimos como punto de referencia el propio soporte, con lo que 
.
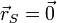Elegimos entonces un sistema de ejes centrado en el soporte con OX el horizontal en el plano del péndulo y OZ el vertical (OY sería perpendicular a ambos e iría hacia el interior de la figura). En este sistema, la posición del centro de masas de la barra (que está en su centro geométrico) vale
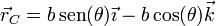
y el momento del peso
El momento cinético es el correspondiente a un eje permanente de rotación.
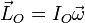
siendo
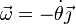
y el momento de inercia respecto del soporte lo podemos hallar por el teorema de Steiner
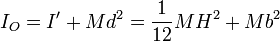
Derivando respecto al tiempo el momento cinético
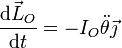
Si igualamos esta derivada al momento de las fuerzas queda la ecuación de movimiento
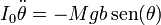
Si el ángulo de desviación es pequeño puede aproximarse el seno por su argumento y escribirse
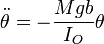
que es la ecuación de un oscilador armónico de frecuencia angular
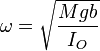
a la cual corresponde un periodo
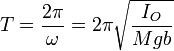
Sustituyendo el valor del momento de inercia queda
