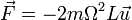Fuerza en anilla ensartada en varillas
De Laplace
| Línea 12: | Línea 12: | ||
<center><math>\vec{F}=m\vec{a}=m\frac{\mathrm{d}^2\vec{r}}{\mathrm{d}t^2}</math></center> | <center><math>\vec{F}=m\vec{a}=m\frac{\mathrm{d}^2\vec{r}}{\mathrm{d}t^2}</math></center> | ||
| + | |||
| + | Podemos hallar esta aceleración derivando dos veces la ecuación anterior. Sin embargo, es más simple aprovechar el que sabemos que describe un movimiento circular uniforme, por lo que su aceleración es igual a | ||
| + | |||
| + | <center><math>\vec{a} = -\omega^2(\vec{r}-\vec{r}_c)=-(2\Omega)^2\left(\frac{L}{2}\right)\vec{u}=-2\Omega^2L\vec{u}</math></center> | ||
| + | |||
| + | siendo <math>\vec{u}</math> un vector unitario radial desde el centro de la circunferencia que describe la anilla. | ||
| + | |||
| + | Por tanto, la fuerza neta será igual a | ||
| + | |||
| + | <center><math>\vec{F}=-2m\Omega^2L\vec{u}</math></center> | ||
==Incluyendo el peso== | ==Incluyendo el peso== | ||
[[Categoría:Problemas de dinámica de la partícula (GIE)]] | [[Categoría:Problemas de dinámica de la partícula (GIE)]] | ||
Revisión de 10:53 26 nov 2011
1 Enunciado
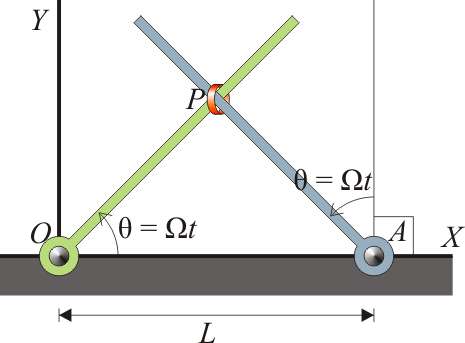
Para el sistema de la anilla ensartada en dos varillas, calcule la fuerza que cada una de las barras ejerce cada instante sobre la anilla, suponiendo ´esta de masa m, (a) despreciando el peso, (b) considerando el peso en la dirección de OY negativo. Tenga en cuenta que cada barra solo puede ejercer fuerza perpendicularmente a sí misma, no a lo largo de ella.
2 Sin considerar el peso
Conocemos el movimiento de la anilla: describe un movimiento circular uniforme en torno al punto medio de los dos anclajes, siendo su velocidad angular 2Ω y el radio de giro L / 2. La ecuación horaria del movimiento es, respecto al anclaje de la izquierda,
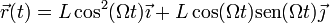
La fuerza neta que actúa sobre la anilla nos la da la segunda ley de Newton
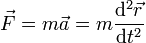
Podemos hallar esta aceleración derivando dos veces la ecuación anterior. Sin embargo, es más simple aprovechar el que sabemos que describe un movimiento circular uniforme, por lo que su aceleración es igual a
siendo 
un vector unitario radial desde el centro de la circunferencia que describe la anilla.
Por tanto, la fuerza neta será igual a
