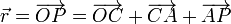Cuestión de cinemática, Noviembre 2011

De Laplace

Revisión de 22:54 20 nov 2011 (ver código fuente) Gabriel (Discusión | contribuciones) (→Ecuación paramétrica de la trayectoria \Gamma.) ← Edición más antigua		Revisión de 22:54 20 nov 2011 (ver código fuente) Gabriel (Discusión | contribuciones) (→Ecuación paramétrica de la trayectoria \Gamma.) Edición más nueva →
Línea 12:		Línea 12:
	Obtendremos la ecuación paramétrica de la trayectoria seguida por el punto <math>P</math>, en términos de la variable geométrica que describe el movimiento de rotación del disco alrededor del punto <math>O</math>: el ángulo <math>\theta</math>. Para ello, descompondremos el radiovector que indica la posición de <math>P</math> respecto de <math>O</math>, en la suma de varios segmentos orientados de descripción sencilla:		Obtendremos la ecuación paramétrica de la trayectoria seguida por el punto <math>P</math>, en términos de la variable geométrica que describe el movimiento de rotación del disco alrededor del punto <math>O</math>: el ángulo <math>\theta</math>. Para ello, descompondremos el radiovector que indica la posición de <math>P</math> respecto de <math>O</math>, en la suma de varios segmentos orientados de descripción sencilla:
-	<math>\vec{r}=\overrightarrow{OP}=\overrightarrow{OC}+\overrightarrow{CA}+\overrightarrow{AP}</math>	+	<center><math>\vec{r}=\overrightarrow{OP}=\overrightarrow{OC}+\overrightarrow{CA}+\overrightarrow{AP}</math></center>

---

Revisión de 22:54 20 nov 2011

1 Enunciado

El mecanismo de la figura consiste en un disco de radio R, siempre contenido en el plano vertical OXY, que se mueve girando alrededor de un punto de su perímetro que coincide con el origen O del sistema de referencia. El movimiento del disco está descrito por la ley horaria θ(t) para el ángulo (medido en radianes) que forma el diámetro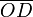 con la dirección horizontal OX. Se considera que el sistema parte de la posición inicial θ = 0. En el punto D hay conectada una cuerda flexible e inextensible de longitud L = πR que, cuando el disco gira, se va enrollando sobre su contorno, finalizando el proceso cuando θ = π. Además, un punto material pesado P hace que el tramo de cuerda no enrollado siempre penda verticalmente.

1. Obtenga la ecuación paramétrica de la trayectoria Γ.
2. El extremo D del diámetro realiza un movimiento circular uniforme, siendo su aceleración 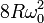. ¿Cómo es la correspondiente ley horaria para el ángulo θ?
3. Calcule la expresión de la componente intrínseca de la velocidad de la partícula P.
4. Aceleración tangencial del punto P.
5. Radio de curvatura de la trayectoria de P en el punto de inicial.

2 Solución

2.1 Ecuación paramétrica de la trayectoria Γ.

Obtendremos la ecuación paramétrica de la trayectoria seguida por el punto P, en términos de la variable geométrica que describe el movimiento de rotación del disco alrededor del punto O: el ángulo θ. Para ello, descompondremos el radiovector que indica la posición de P respecto de O, en la suma de varios segmentos orientados de descripción sencilla: